Introduction to Flix

Flix is a principled functional, logic, and imperative programming language developed at Aarhus University and by a community of open source contributors in collaboration with researchers from the University of Waterloo, from the University of Tubingen, and from the University of Copenhagen.

Flix is inspired by OCaml and Haskell with ideas from Rust and Scala. Flix looks like Scala, but its type system is based on Hindley-Milner which supports complete type inference. Flix is a state-of-the-art programming language with multiple innovative features, including:

• a polymorphic type and effect system with full type inference.
• region-based local mutable memory.
• user-defined effects and handlers.
• higher-kinded traits with associated types and effects.
• embedded first-class Datalog programming.

Flix compiles to efficient JVM bytecode, runs on the Java Virtual Machine, and supports full tail call elimination. Flix has interoperability with Java and can use JVM classes and methods. Hence the entire Java ecosystem is available from within Flix.

Flix aims to have world-class Visual Studio Code support. The Flix Visual Studio Code extension uses the real Flix compiler hence there is always a 1:1 correspondence between the Flix language and what is reported in the editor. The advantages are many: (a) diagnostics are always exact, (b) code navigation “just works”, and (c) refactorings are always correct.

Look and Feel

Here are a few programs to illustrate the look and feel of Flix:

This program illustrates the use of algebraic data types and pattern matching:

/// An algebraic data type for shapes.
enum Shape {
    case Circle(Int32),          // circle radius
    case Square(Int32),          // side length
    case Rectangle(Int32, Int32) // height and width
}

/// Computes the area of the given shape using
/// pattern matching and basic arithmetic.
def area(s: Shape): Int32 = match s {
    case Shape.Circle(r)       => 3 * (r * r)
    case Shape.Square(w)       => w * w
    case Shape.Rectangle(h, w) => h * w
}

// Computes the area of a 2 by 4.
def main(): Unit \ IO =
    area(Shape.Rectangle(2, 4)) |> println

Here is an example that uses polymorphic records:

/// Returns the area of the polymorphic record `r`.
/// Note that the use of the type variable `a` permits the record `r`
/// to have labels other than `x` and `y`.
def polyArea[a : RecordRow](r: {x = Int32, y = Int32 | a}): Int32 = r#x * r#y

/// Computes the area of various rectangle records.
/// Note that some records have additional labels.
def polyAreas(): List[Int32] =
    polyArea({x = 1, y = 2}) ::
    polyArea({x = 2, y = 3, z = 4}) :: Nil

def main(): Unit \ IO =
    polyAreas() |> println

Here is an example that uses region-based local mutation:

///
/// We can define pure functions that use
/// internal mutability (impurity) with regions.
/// Regions encapsulate mutability to its declared scope.
///
def deduplicate(l: List[a]): List[a] with Order[a] =
    /// Declare a new region `rc`.
    region rc {

        /// Create a new `MutSet` at region `r`.
        /// This will be used to keep track of
        /// unique elements in `l`.
        let s = MutSet.empty(rc);

        /// The lambda used in the call to `filter`
        /// would be impure without a region.
        List.filter(x -> {
            if (MutSet.memberOf(x, s))
                false // `x` has already been seen.
            else {
                MutSet.add(x, s);
                true
            }
        }, l)
    }

Here is an example that uses built-in effects and handlers:

use Net.Http
use Net.Retry
use Net.HttpResponse
use Time.Clock
use Time.Duration.{milliseconds, seconds}

def main(): Unit \ { Clock, Http, Logger, IO } =
    let defaultHeaders = Map#{
        "Accept"        => List#{"application/json"},
        "Authorization" => List#{"Bearer tok123"}
    };
    run {
        let urls = List#{"/api/users", "/api/posts"};
        foreach (url <- urls) {
            match Http.get(url) {
                case Ok(resp) => println("${url} -> ${HttpResponse.status(resp)}")
                case Err(err) => println("${url} -> ${err}")
            }
        };
        match Http.get("https://notfound.flix.dev/") {
            case Ok(resp) => println("notfound -> ${HttpResponse.status(resp)}")
            case Err(err) => println("notfound -> ${err}")
        }
    } with Http.withBaseUrl("https://flix.dev")
      with Http.withDefaultHeaders(defaultHeaders)
      with Http.withRetry(Retry.linear(maxRetries = 2, delay = milliseconds(100)))
      with Http.withCircuitBreaker(failureThreshold = 3, cooldown = seconds(5))
      with Http.withSlidingWindow(maxRequests = 2, window = seconds(1))
      with Http.withLogging

Here is an example that defines its own effects and handlers:

eff MyPrint {
    def println(s: String): Unit
}

eff MyTime {
    def getCurrentHour(): Int32
}

def sayGreeting(name: String): Unit \ {MyPrint, MyTime} = {
    let hour = MyTime.getCurrentHour();
    if (hour < 12)
        MyPrint.println("Good morning, ${name}")
    else
        MyPrint.println("Good afternoon, ${name}")
}

def main(): Unit \ IO =
    run {
        (sayGreeting("Mr. Bond, James Bond"): Unit)
    } with handler MyPrint {
        def println(s, k) = { println(s); k() }
    } with handler MyTime {
        def getCurrentHour(_, k) = k(11)
    }

Here is an example that uses first-class Datalog constraints:

def reachable(edges: List[(Int32, Int32)], src: Int32, dst: Int32): Bool =
    let db = inject edges into Edge/2;
    let pr = #{
        Path(x, y) :- Edge(x, y).
        Path(x, z) :- Path(x, y), Edge(y, z).
        Reachable() :- Path(src, dst).
    };
    let result = query db, pr select () from Reachable();
    not Vector.isEmpty(result)

And finally here is an example that uses structured concurrency with channels and processes:

/// A function that sends every element of a list
def sendAll(l: List[Int32], tx: Sender[Int32]): Unit \ Chan =
    match l {
        case Nil     => ()
        case x :: xs => Channel.send(x, tx); sendAll(xs, tx)
    }

/// A function that receives n elements
/// and collects them into a list.
def recvN(n: Int32, rx: Receiver[Int32]): List[Int32] \ {Chan, NonDet} =
    match n {
        case 0 => Nil
        case _ => Channel.recv(rx) :: recvN(n - 1, rx)
    }

/// A function that calls receive and sends the result on d.
def wait(rx: Receiver[Int32], n: Int32, tx: Sender[List[Int32]]): Unit \ {Chan, NonDet} =
    Channel.send(recvN(n, rx), tx)

/// Spawn a process for send and wait, and print the result.
def main(): Unit \ {Chan, NonDet, IO} = region rc {
    let l = 1 :: 2 :: 3 :: Nil;
    let (tx1, rx1) = Channel.buffered(100);
    let (tx2, rx2) = Channel.buffered(100);
    spawn sendAll(l, tx1) @ rc;
    spawn wait(rx1, List.length(l), tx2) @ rc;
    println(Channel.recv(rx2))
}

Additional examples can be found in these pages and in the examples folder on GitHub.

Getting Started

Getting started with Flix is straightforward. All you need is Java version 21+.

You can check if Java is installed and its version by typing:

$ java -version

which should print something like:

openjdk version "21" 2023-09-19 LTS
OpenJDK Runtime Environment Temurin-21+35 (build 21+35-LTS)
OpenJDK 64-Bit Server VM Temurin-21+35 (build 21+35-LTS, mixed mode, sharing)

If Java is not installed or your version is too old, a newer version can be downloaded from Adoptium.

Once you have Java 21+ installed there are two ways to proceed:

• You can use the Flix VSCode extension (highly recommended) or
• You can run the Flix compiler from the command line.

Using Flix from VSCode

Flix comes with a fully-featured VSCode plugin. Follow these steps to get started:

1. Create a new empty folder (e.g. my-flix-project).
2. Open VSCode and choose File -> Open Folder.
3. Create a new file called Main.flix in the folder.
4. VSCode will ask you want to search the marketplace for extensions. Say “Yes”.
5. The Flix extension will be downloaded and installed. Once done, it will ask if you want to download the Flix compiler. Say “Yes” again.
6. When you see “Starting Flix” followed by “Flix Ready!” everything should be ready.

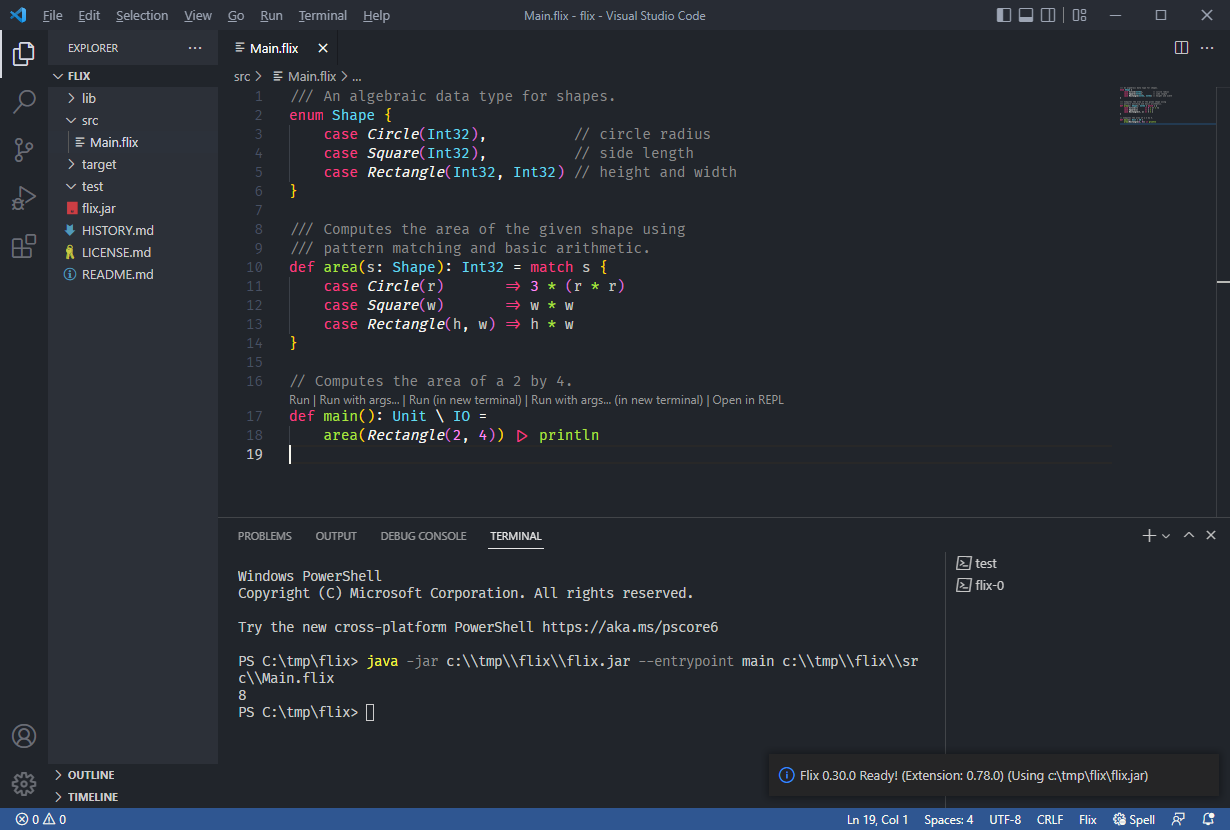
A screenshot of the Flix Visual Studio Code extension in action:

Using Flix from Neovim

Flix can also be used from Neovim. Follow these steps to get started:

• the official plugin relies on features released in Neovim 0.11
• check the version of neovim installed

nvim --version

Neovim Plugin

There is a Lua plugin which provides an LSP configuration for the native neovim lsp, and several functions to interact with the flix cli. It’s repo has detailed installation and configuration instructions. It can be installed with a plugin manager of choice or cloned locally into your neovim runtime path.

The plugin provides no Keymappings but sets the Flix LSP server up, allowing it to work with your default LSP mappings. An example of setting up LSP keymappings with nvim 0.11 can be seen below. Once your LspAttach autocmd has been set the keymappings will apply to all configured lsp servers.

-- create auto command that is triggered when your LSP server attatches to the buffer
vim.api.nvim_create_autocmd('LspAttach', {
  -- give it a name to prevent autocmd conflicts
  group = vim.api.nvim_create_augroup('my.lsp', {}),
  -- the function to run when the server attatches
  callback = function(args)
    -- helper function to set keybinding options with an optional description string
    -- !!! important !!!
    -- `buffer` makes these mappings local to the buffer triggering the autocmd
    local function get_opts(desc)
      return { desc = desc, buffer = args.buf, noremap = true, silent = true }
    end
    -- check that the LSP client supports features before setting bindings
    local client = assert(vim.lsp.get_client_by_id(args.data.client_id))
    if client:supports_method('textDocument/format') then
      vim.keymap.set('n', '<leader>=', vim.lsp.buf.format, get_opts('format buffer'))
    end
    if client:supports_method('textDocument/rename') then
      vim.keymap.set('n', '<leader>rn', vim.lsp.buf.rename, get_opts('rename'))
    end
    vim.keymap.set("n", "<leader>ca", vim.lsp.buf.code_action, get_opts("lsp code action"))
    vim.keymap.set("n", "<leader>cl", vim.lsp.codelens.run, get_opts("lsp codelens run"))
    vim.keymap.set("n", "gr", vim.lsp.buf.references, get_opts("lsp references"))
    vim.keymap.set("n", "gd", vim.lsp.buf.definition, get_opts("lsp definition"))
    vim.keymap.set("n", "<leader>h", vim.lsp.buf.document_highlight, get_opts("lsp document highlight"))
    vim.keymap.set("n", "K", vim.lsp.buf.hover, get_opts("lsp hover"))
    vim.keymap.set("n", "gi", vim.lsp.buf.implementation, get_opts("lsp buf implementation"))
    vim.keymap.set('i', '<C-a>', '<C-x><C-o>', get_opts("manual expand completion"))
    vim.keymap.set("n", "<leader>rn", vim.lsp.buf.rename, get_opts(""))
    vim.keymap.set("n", "<leader>d", vim.diagnostic.open_float, get_opts("diagnostic open float"))
    vim.keymap.set("n", "<leader>ws", vim.lsp.buf.workspace_symbol, get_opts("lsp workspace symbol"))
    vim.keymap.set("n", "<leader>ds", vim.lsp.buf.document_symbol, get_opts("lsp doc symbol"))
  end
})

The snippet above provides the following keybindings.

Previously lspconfig provided LSP functionality to neovim and lsp configurations. However, after version 0.11 neovim has LSP built in, lspconfig only provides configurations for common lsp servers. This makes its installation less necessary but it is still recommended.

Manual Configuration

If you would rather setup the LSP server yourself the code from the plugin is as follows.

1. Tell nvim what filetypes are Flix files

vim.filetype.add({
  extension = {
    flix = "flix",
  }
})

2. Configure the Flix LSP for neovim’s native LSP client

-- check if "flix" has already been setup
if not vim.lsp.config["flix"] then
  -- create flix LSP configuration for native LSP
  vim.lsp.config('flix', {
    -- choose just one `cmd` definition
    -- for a project local `flix.jar` ie flix.jar is installed in the root of your project
    cmd = { "java", "-jar", "flix.jar", "lsp" },
    -- for a global flix installation ie with "homebrew" or "nix"
    cmd = {"flix", "lsp"},
    filetypes = { "flix" },
    root_markers = { "flix.toml" }, -- where to set the root directory
    cmd_cwd = vim.fs.root(0, { 'flix.toml' }),
    root_dir = vim.fs.root(0, { 'flix.toml' }),
})
end

3. Create an autocmd to set flix defualts such as comments and indenting, and to run the codelens whenever your flix buffer changes.

-- auto commands
-- create named "groups" to prevent autocmd conflicts
local flix = vim.api.nvim_create_augroup("flix.ft", { clear = true })
local flix_lsp = vim.api.nvim_create_augroup("flix.lsp", { clear = true })
-- autocmd that activates when a "flix" buffer is entered
vim.api.nvim_create_autocmd("FileType", {
  group = flix,
  pattern = "flix",
  callback = function(args)
    vim.api.nvim_clear_autocmds({ group = flix_lsp, buffer = args.buf }) -- prevent duplicates
    -- set flix defaults
    vim.opt_local.tabstop = 4
    vim.opt_local.shiftwidth = 4
    vim.opt_local.softtabstop = 4
    vim.bo.commentstring = "// %s"
    -- refresh codelens
    vim.api.nvim_create_autocmd({ 'BufEnter', 'CursorHold', 'InsertLeave' }, {
      group = flix_lsp,
      buffer = args.buf,
      callback = function()
        vim.lsp.codelens.refresh({ bufnr = args.buf })
      end
    })
  end
})

place this code in your $HOME/.config/nvim/init.lua or wherever you configure your lsp in neovim.

Using Flix from Emacs

Flix can be used from Emacs as well by installing the flix-mode package. Follow the instructions there to get started writing Flix code in Emacs.

Using Flix from the CLI

Flix can also be used from the command line. Follow these steps:

1. Create a new empty folder (e.g. my-flix-project).
2. Download the latest flix.jar from https://github.com/flix/flix/releases/latest and put it into the folder.
3. Enter the created directory (e.g. cd my-flix-project) and run java -jar flix.jar init to create an empty Flix project.
4. Run java -jar flix.jar run to compile and run the project.

Installing Flix with Nix

Flix can also be installed using the nix package manager. To install for the currently running shell run:

$ nix-shell -p flix

Or alternatively to install globally:

$ nix-env -i flix

Then run flix run in your project directory.

Troubleshooting

The most common reasons for Flix not working are (a) the java command not being on your PATH, (b) the JAVA_HOME environmental variable not being set or being set incorrectly, or (c) having the wrong version of Java installed. To debug these issues, ensure that:

• The command java -version prints the right Java version.
• The JAVA_HOME environmental variable is correctly set.
  • On Windows, you can print the variable by typing echo %JAVA_HOME%.
  • On Mac and Linux, you can print the variable by typing echo $JAVA_HOME.

If you are still stuck, you can ask for help on Gitter.

Hello World

We can now see the famous Hello World program in src/Main.flix file:

def main(): Unit \ IO = 
    println("Hello World!")

That’s it!

You will immediately notice a few things are different from other programming languages:

• The main function has no formal parameters, in particular it does not take an arguments array. Instead the command line arguments are available through the Env effect (see The Main Function).
• The return type of the main function is Unit.
• The main function has the IO effect since it prints to the terminal.

Next Steps

We are now ready write our first real program!

We will write a simple variant of the venerable wordcount (wc) program from UNIX.

We will use the opportunity to illustrate how to use algebraic effects in Flix.

use Fs.FileRead

def wc(file: String): Unit \ { FileRead, IO } =
    match FileRead.readLines(file) {
        case Ok(lines) =>
            let totalLines = List.length(lines);
            let totalWords = List.sumWith(numberOfWords, lines);
            println("Lines: ${totalLines}, Words: ${totalWords}")
        case Err(_) =>
            println("Unable to read file: ${file}")
    }

def numberOfWords(s: String): Int32 =
     s |> String.words |> List.length

def main(): Unit \ { FileRead, IO } =
    wc("Main.flix")

The program works as follows:

We define a wc function that takes a filename and reads all lines from the file using the FileRead effect.

If the file is successfully read, we calculate:

• The number of lines using List.length.
• The number of words by summing the results of applying numberOfWords to each line.

The results are printed to the terminal using println.

If the file cannot be read, an error message is printed instead.

The wc function’s type and effect signature specifies the {FileRead, IO} effect set, indicating these effects are required. Both FileRead and IO have default handlers, so no explicit handler calls are needed in main.

Data Types

Flix comes with a collection of built-in data types, such as booleans, floats and integers, and compound types, such as tuples and records. Moreover, the standard library defines types such as Option[a], Result[e, t], List[a], Set[a], and Map[k, v].

In addition to these types, Flix allows programmers to define their own types, including enumerated types, recursive types, and polymorphic types.

Flix also supports type aliases (new types).

Primitives

Flix supports the primitive types:

Float64 and Int32 values can be written without suffix, i.e. 123.0f64 can simply be written as 123.0 and 123i32 can be written as 123.

Literals

Flix has built-in syntactic sugar for lists, sets, maps and regex.

List Literals

A list literal is written using the infix :: constructor. For example:

1 :: 2 :: 3 :: Nil

which is syntactic sugar for:

Cons(1, Cons(2, Cons(3, Nil)))

Alternatively, the same list can also be written as:

List#{1, 2, 3}

Set Literals

A set literal is written using the notation Set#{v1, v2, ...}. For example:

Set#{1, 2, 3}

which is syntactic sugar for:

Set.insert(3, Set.insert(2, Set.insert(1, Set.empty())))

Note that the elements are inserted from left to right, thus 1 is inserted first.

Map Literals

A map literal is written using the notation Map#{k1 => v1, k2 => v2, ...}. For example:

Map#{1 => "Hello", 2 => "World"}

which is syntactic sugar for:

Map.insert(2, "World", Map.insert(1, "Hello", Map.empty()))

Note that similar to sets above, the entries are inserted left to right. In particular, if multiple entries share the same key, the rightmost one overwrites the previous values.

Regex Literals

A regex literal is written using the notation regex"...". For example:

Regex.isMatch(regex"abc", "abc")

Additionally, regex literals support regex escape sequences with the following notation regex"\\...". For example:

Regex.isMatch(regex"\\w", "W")

1. More precisely, a Char value corresponds to a single UTF-16 code unit. UTF-16 is a variable length encoding: some of the Unicode code points are represented by a single UTF-16 code unit, but others need two code units. (Also note that a combination of several Unicode code points may be needed to represent what is usually perceived as a single character.) ↩

Tuples

A tuple is a product of values. The form of a tuple is (exp1, ..., expn).

For example, here is a 2-tuple (a pair) of an Int32 and a Bool:

(123, true)

The type of the tuple is (Int32, Bool).

We can destructure a tuple using pattern matching. For example:

let t = ("Lucky", "Luke", 42, true); // 4-tuple
let (fstName, lstName, age, male) = t;
lstName

evaluates to the string "Luke".

The Flix Prelude defines the fst and snd functions:

let t = (1, 2);
let x = fst(t); // x = 1
let y = snd(t)  // y = 2

which are useful when working with 2-tuples (i.e. pairs). For example:

let l = (1, 1) :: (2, 2) :: Nil; // has type List[(Int32, Int32)]
List.map(fst, l)                 // has type List[Int32]

which evaluates to the list:

1 :: 2 :: Nil

Enums

Enumerated Types

Enumerated types are used to define a type that has a finite (enumerated) set of values. Enumerated types are useful for things such as modeling compass directions, the cards in a deck, and the days in a week.

For example, here is an enumeration of the days in a week:

enum Weekday {
    case Monday,
    case Tuesday,
    case Wednesday,
    case Thursday,
    case Friday,
    case Saturday,
    case Sunday
}

Here Monday, Tuesday and so on are referred to as the constructors of the enum.

We can refer to a weekday as Monday or Weekday.Monday. The latter is required if we have multiple enums in scope with similarly named constructors.

We can use pattern matching to destruct an enum value. For example:

enum Animal {
    case Cat,
    case Dog,
    case Giraffe
}

def isTall(a: Animal): Bool = match a {
    case Animal.Cat        => false
    case Animal.Dog        => false
    case Animal.Giraffe    => true
}

The function isTall takes a value of type Animal and performs a pattern match on it. If the value is Giraffe the function returns true. Otherwise it returns false.

Flix guarantees that pattern matches are exhaustive, i.e. that all cases have been covered. It is a compile-time error if a pattern match is non-exhaustive. A pattern match can always be made exhaustive by adding a default case as the last case. A default case is written with an underscore case _ => ???.

Recursive Types

Recursive types are used to define types that are self-referential.

For example, we can define a binary tree of integers as follows:

enum Tree {
    case Leaf(Int32),
    case Node(Tree, Tree)
}

A tree is either a Leaf with an Int32 value or an internal Node with a left and a right sub-tree. Note that the definition of Tree refers to itself.

We can write a function, using pattern matching, to compute the sum of all integers in such a tree:

def sum(t: Tree): Int32 = match t {
    case Tree.Leaf(x)    => x
    case Tree.Node(l, r) => sum(l) + sum(r)
}

The sum function pattern matches on a tree value. If the tree is a leaf its value is simply returned. Otherwise the function recurses on both subtrees and adds their results.

Polymorphic Types

Polymorphic types are types parameterized by other types. For example, we can write:

enum Bottle[a] {
    case Empty,
    case Full(a)
}

def isEmpty(b: Bottle[a]): Bool = match b {
    case Bottle.Empty   => true
    case Bottle.Full(_) => false
}

Here the Bottle type is parameterized by the type parameter a. In Flix, type parameters, like ordinary parameters are always written in lowercase. The Bottle type has two cases: either the bottle is empty (and contains no value) or it is full (and contains one value of type a). The isEmpty function takes a bottle, type parameterized by a, and determines if the bottle is empty.

The careful reader might have noticed that Bottle is equivalent to the more well-known Option type.

In general, polymorphic types can have more than one type argument. For example, the standard library implement of the Result has two type parameters:

enum Result[e, t] {
    case Ok(t),
    case Err(e)
}

Shorthand Enum Syntax

A typical enum may look like:

enum Weekday {
    case Monday,
    case Tuesday,
    case Wednesday,
    case Thursday,
    case Friday,
    case Saturday,
    case Sunday
}

The same enum can also be declared as:

enum Weekday {
    case Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday
}

This shorthand syntax is always available, but should only be used for simple enums.

Singleton Enum Syntax

An enum with a single case:

enum USD {
  case USD(Int32)
}

can be shortened to:

enum USD(Int32)

Type Aliases

Type aliases introduces a short-hand name for a type. For example:

///
/// A type alias for a map from keys of type `k`
/// to values of type `Result[String, v]`
///
type alias M[k, v] = Map[k, Result[String, v]]

def foo(): M[Bool, Int32] = Map#{true => Ok(123)}

A type alias does not define a new distinct type. Rather a type alias is simply a syntactic short-hand for a (usually complex) type.

The Flix compiler expands type aliases before type checking. Consequently, type errors are always reported with respect to the actual underlying types.

Note: A type alias cannot be recursively defined in terms of itself. The Flix compiler will detect and report such recursive cycles.

Functions

Functions and higher-order functions are the key building block of a functional programming language.

In Flix, top-level functions are defined with the def keyword. For example:

def add(x: Int32, y: Int32): Int32 = x + y + 1

A definition consists of the function name followed by an argument list, the return type, and the function body. Although Flix supports type inference, top-level function definitions must declare the type of their arguments and their return type.

In Flix, all function arguments and local variables must be used. If a function argument is not used it must be prefixed with an underscore to explicitly mark it as unused.

Higher-Order Functions

A higher-order function is a function that takes a parameter which is itself a function. For example:

def twice(f: Int32 -> Int32, x: Int32): Int32 = f(f(x))

Here the twice function takes two arguments, a function f and an integer x, and applies f to x two times.

We can pass a lambda expression to the twice function:

twice(x -> x + 1, 42)

which evaluates to 44 since 42 is incremented twice.

We can also define a higher-order function that requires a function which takes two arguments:

def twice(f: (Int32, Int32) -> Int32, x: Int32): Int32 =
    f(f(x, x), f(x, x))

which can be called as follows:

twice((x, y) -> x + y, 42)

We can call a higher-order function with a top-level function as follows:

def inc(x: Int32): Int32 = x + 1

def twice(f: Int32 -> Int32, x: Int32): Int32 = f(f(x))

twice(inc, 42)

Function Type Syntax

Depending on the number of arguments to a function, the syntax for the function type differs:

Unit -> Int32                // For nullary functions
Int32 -> Int32               // For unary functions
(Int32, Int32, ...) -> Int32 // For the rest

Function Composition

Flix supports several operators for function composition and pipelining:

let f = x -> x + 1;
let g = x -> x * 2;
let h = f >> g;     // equivalent to x -> g(f(x))

Here >> is forward function composition.

We can also write function applications using the pipeline operator:

List.range(1, 100) |>
List.filter(x -> x `Int32.mod` 2 == 0) |>
List.map(x -> x * x) |>
println;

Here x |> f is equivalent to the function application f(x).

Curried by Default

Functions are curried by default. A curried function can be called with fewer arguments than it declares returning a new function that takes the remainder of the arguments. For example:

def sum(x: Int32, y: Int32): Int32 = x + y

def main(): Unit \ IO =
    let inc = sum(1);
    inc(42) |> println

Here the sum function takes two arguments, x and y, but it is only called with one argument inside main. This call returns a new function which is similar to sum, except that in this function x is always bound to 1. Hence when inc is called with 42 it returns 43.

Currying is useful in many programming patterns. For example, consider the List.map function. This function takes two arguments, a function of type a -> b and a list of type List[a], and returns a List[b] obtained by applying the function to every element of the list. Now, if we combine currying with the pipeline operator |> we are able to write:

def main(): Unit \ IO =
    List.range(1, 100) |>
    List.map(x -> x + 1) |>
    println

Here the call to List.map passes the function x -> x + 1 which returns a new function that expects a list argument. This list argument is then supplied by the pipeline operator |> which, in this case, expects a list and a function that takes a list.

Pipelines

Flix supports the pipeline operator |> which is simply a prefix version of function application (i.e. the argument appears before the function).

The pipeline operator can often be used to make functional code more readable. For example:

let l = 1 :: 2 :: 3 :: Nil;
l |>
List.map(x -> x * 2) |>
List.filter(x -> x < 4) |>
List.count(x -> x > 1)

Here is another example:

"Hello World" |> String.toUpperCase |> println

Operators

Flix has a number of built-in unary and infix operators. In addition Flix supports infix function application by enclosing the function name in backticks. For example:

123 `sum` 456

is equivalent to the normal function call:

sum(123, 456)

In addition, a function named with an operator name (some combination of +, -, *, <, >, =, !, &, |, ^, and $) can also be used infix. For example:

def <*>(x: Int32, y: Int32): Int32 = ???

can be used as follows:

1 <*> 2

Immutable Data

The bread-and-butter of functional programming is immutable data types.

We have already seen several examples of immutable data types:

• Primitive Types
• Tuple Types
• Enumerated, Recursive, and Polymorphic Types

In addition, The Flix standard library offers several immutable data types:

• List[t] : An immutable singly-linked list of elements of type t.
• Chain[t] : An immutable chain of elements of type t with fast append.
• Vector[t] : An immutable sequence of elements of type t with fast lookup.
• Set[t] : An immutable set of elements of type t.
• Map[k, v] : An immutable map of keys of type k to values of type v.

Other immutable data types include:

• Option[t] : A type that is either None or Some(t).
• Result[e, t] : A type that is either Ok(t) or Err(e).
• Nel[t] : An immutable non-empty singly-linked list of elements of type t.
• Nec[t] : An immutable non-empty sequence of elements of type t that supports fast append.
• MultiMap[k, v] : An immutable map of keys of type k to sets of values of type v.

Lists

A list is either the empty list, written as Nil, or a cons cell, written as x :: xs where x is the head element and xs is the tail of the list. The List type is polymorphic so you can have a list of integers, written as List[Int32], or a list of strings written as List[String].

We write the empty list as follows:

Nil

We can construct a list of strings with the strings "Hello" and "World" as follows:

"Hello" :: "World" :: Nil

or using the following notation:

List#{"Hello", "World"}

Given a list there are many useful operations we can perform on it.

For example, we can compute the length of a list as follows:

List.length(1 :: 2 :: 3 :: Nil)

We can also reverse the order of elements in a list:

List.reverse(1 :: 2 :: 3 :: Nil)

We can append two lists using the List.append function as follows:

let xs = (1 :: 2 :: 3 :: Nil);
let ys = (4 :: 5 :: 6 :: Nil);
List.append(xs, ys)

Or, alternatively, we can use the built-in append operator ::: as follows:

let xs = (1 :: 2 :: 3 :: Nil);
let ys = (4 :: 5 :: 6 :: Nil);
xs ::: ys

Flix has an extensive collection of functions to operate on lists.

Here are some of the most common:

List.count(x -> x == 1, 1 :: 2 :: 3 :: Nil);
List.filter(x -> x == 1, 1 :: 2 :: 3 :: Nil);
List.map(x -> x + 1, 1 :: 2 :: 3 :: Nil);
List.foldLeft((x, y) -> x + y, 0, 1 :: 2 :: 3 :: Nil)

And here are some more exotic functions:

List.intersperse("X", "a" :: "b" :: "c" :: Nil)

which inserts "X" between every element in the list.

let l1 = "X" :: "Y" :: Nil;
let l2 = ("a" :: "b" :: Nil) :: ("c" :: "d" :: Nil) :: Nil;
List.intercalate(l1, l2)

which inserts the list l1 between every element in the list l2.

We can write our own recursive functions to operate on lists.

For example, here is an implementation of the map function:

///
/// Returns the result of applying `f` to every element in `l`.
/// That is, the result is of the form: `f(x1) :: f(x2) :: ...`.
///
pub def map(f: a -> b \ ef, l: List[a]): List[b] \ ef = match l {
    case Nil     => Nil
    case x :: xs => f(x) :: map(f, xs)
}

Chains and Vectors

In addition to immutable Lists, Flix also supports immutable Chains and Vectors.

The following table illustrates the performance trade-offs between lists, chains, and vectors:

When to use List, Chain, or Vector?:

• The List data structure should be the default choice as it is simple and well-known.
• The Vector data structure is an excellent choice when the size of a collection is fixed and/or when fast random access is required.
• The Chain data structure is more rarely used, but shines when fast appends are required.

Chains

A Chain[t] is an immutable linked sequence of elements.

The Chain[t] data type is defined as:

enum Chain[t] {
    case Empty
    case One(t)
    case Chain(Chain[t], Chain[t])
}

The data structure supports O(1) append because we can construct a new chain from two existing chains using the Chain constructor (or more appropriately using Chain.append).

We can build chains using Chain.empty, Chain.singleton, Chain.cons, and Chain.append.

For example, we can write:

let c = Chain.cons(1, Chain.empty());
println(c)

which prints Chain#{1} when compiled and executed.

Vectors

A Vector[t] is an immutable fixed-length sequence of contiguous elements of type t.

Flix has support for Vector literals. For example, we can write:

Vector#{1, 2, 3}

which creates a vector of length three with the elements: 1, 2, and 3.

Vectors support fast random access with the Vector.get operation:

let v = Vector#{1, 2, 3};
println(Vector.get(2, v))

which prints 3 when compiled and executed.

Warning: Indexing into a vector beyond its bounds will panic the program.

Vectors support many operations. For example, we can map a function over a vector:

let v = Vector#{1, 2, 3};
Vector.map(x -> x + 1, v)

evaluates to Vector#{2, 3, 4}.

Sets and Maps

Flix has excellent support for (immutable) Sets and Map based on balanced trees; hence the elements of a Set and the keys of Map must implement the Order trait.

Tip: The Flix Set and Map data structures will automatically parallelize certain operations. Such operations are marked with @ParallelWhenPure in the API docs.

Sets

The empty set is written as:

Set#{}

which is equivalent to Set.empty(). A set literal is written as:

Set#{1, 2, 3}

We can insert into a set using Set.insert (which returns a new set):

let s1 = Set#{1, 2, 3};
let s2 = Set.insert(4, s1);

We can determine if a set contains an element using Set.memberOf:

let s = Set#{1, 2, 3};
Set.memberOf(2, s)

We can merge two sets using Set.union:

let s1 = Set#{1, 2, 3};
let s2 = Set#{3, 4, 5};
let sr = Set.union(s1, s2);

Since Sets are SemiGroups, we can also use the ++ operator and write s1 ++ s2.

Maps

The empty map is written as:

Map#{}

which is equivalent to Map.empty(). A map literal is written as:

Map#{"a" => 1, "b" => 2, "c" => 3}

We can insert into a map using Map.insert (which returns a new map):

let m1 = Map#{"a" => 1, "b" => 2, "c" => 3};
let m2 = Map.insert("d", 4, m1);

We can lookup the value associated with a key using Map.get:

let m = Map#{"a" => 1, "b" => 2, "c" => 3};
Map.get("b", m) 

The Map.get function returns an Option[v].

We can merge two maps using one of Map.unionWith and Map.unionWithKey functions.

Records

Flix supports row polymorphic extensible records.

Flix records are immutable (but may contain mutable reference cells).

Record Literals

A record literal is written with curly braces:

{ x = 1, y = 2 }

which has the record type { x = Int32, y = Int32 }.

The order of labels in a record does not matter. Hence the above record is equivalent to:

{ y = 2, x = 1 }

which has type { y = Int32, x = Int32 }. This type is equivalent to { x = Int32, y = Int32 }. In other words, the order of labels within a record type does not matter.

Label Access

We can access the label of a record using a hash:

let p = { x = 1, y = 2 };
p#x + p#y

The type system ensures that we cannot access a label that does not exist.

Records are immutable. Once constructed, the values of the record labels cannot be changed.

Label Update

While records are immutable, we can construct a new record with an updated label value:

let p1 = { x = 1, y = 2 };
let p2 = { x = 3 | p1 };
p1#x + p2#x

The expression { x = 3 | p1 } updates the record p1 with a new value of its x label. Note that updating a label requires that the label exists on the record. A record cannot be updated with a new label, but it can be extended with a new label, as we shall see later.

Record Extension

We can add a new label to an existing record as follows:

let p1 = { x = 1, y = 2 };
let p2 = { +z = 3 | p1 };
p1#x + p1#y + p2#z

Here the expression { +z = 3 | p1 } extends the record p1 with a new label z such that the result has three labels: x, y, and z all of which are of Int32 type.

Record Restriction

Similarly to record extension, we can also remove a label from a record:

let p1 = { x = 1, y = 2 };
let p2 = { -y | p1 };

Here the record p2 has the same labels as p1 except that the y label has been removed.

Row Polymorphism

A function may specify that it requires a record with two labels:

def f(r: {x = Int32, y = Int32}): Int32 = r#x + r#y

We can call this function with the records { x = 1, y = 2 } and { y = 2, x = 1 }, but we cannot call it with the record { x = 1, y = 2, z = 3 } since the signature of f demands a record with exactly two labels: x and y. We say that the record r is closed.

We can lift this restriction by using row polymorphism:

def g(r: {x = Int32, y = Int32 | s}): Int32 = r#x + r#y

We can call this function with any record as long as it has x and y labels which are of type Int32. We say that the record type of r is open.

Named Parameters

When a function has multiple parameters that share the same type, it is easy to get confused about the right argument order. For example, what does String.contains("Hello","Hello World") return? What does String.contains("Hello World", "Hello") return?

A common solution to this problem is to use named parameters. Flix supports a form of named parameters building on records. For example, we can write a function translate to translate from one language to another as follows:

def translate(src: {src = Language}, dst: {dst = Language}, text: String): String = ???

We can call this function as follows:

translate({src = English}, {dst = French}, "Where is the library?")

Since such verbosity gets tedious, we can also use the syntactic sugar:

translate(src = English, dst = French, "Where is the library?")

which is equivalent to the above.

Mutable Data

Flix is a functional-first programming language that encourages but does not demand, the use of immutable data structures. While immutable data structures should be the default, Flix has rich support for imperative programming with destructive updates to mutable data.

Flix uses its effect system to separate pure and impure code. In particular, Flix uses the region concept to track the use of mutable memory. That is, all mutable memory belongs to some statically-scoped region.

Flix has three basic types of mutable memory:

• References
• Arrays
• Structs

We can use these data types to build higher-level mutable data structures. For example, the Flix Standard Library offers collections such as MutList, MutDeque, MutSet, and MutMap. As a rule, these higher-level data structures should be preferred over lower-level references and arrays.

We begin this chapter with a discussion of regions.

Regions

Flix supports scoped mutable memory. In Flix, all mutable memory belongs to a region that is tied to its lexical scope. When execution leaves the lexical scope of a region, all memory in that region becomes unreachable.

Regions are useful because they enable us to implement pure functions that internally use mutation. We will illustrate this powerful idea with several real-world examples, but let us first discuss how to use a region:

We introduce a new region scope with the region construct:

region rc { // region starts.
  ...       // the region handle `rc` is in scope.
}           // region ends and all data associated with `rc` is no longer in scope.

We can use regions to implement a pure sort function that internally uses mutation:

def sort(l: List[a]): List[a] with Order[a] =
    region rc {
        let arr = List.toArray(rc, l);
        Array.sort(arr);
        Array.toList(arr)
    }

Here we introduce a region named rc. We use the function List.toArray to convert the list l to a mutable array arr associated with the region rc. We then sort arr using Array.sort which uses an efficient in-place sorting algorithm. Finally, we convert the sorted array back to a list and return it. The sort function is pure, even though it internally uses mutation.

As another example, we can implement a toString function for List[a] which is pure but internally uses a mutable StringBuilder:

def toString(l: List[a]): String with ToString[a] =
    region rc {
        let sb = StringBuilder.empty(rc);
        List.forEach(x -> StringBuilder.appendString("${x} :: ", sb), l);
        StringBuilder.appendString("Nil", sb);
        StringBuilder.toString(sb)
    } // scope of rc ends, the entire expression is pure.

The programming pattern is the same: We open a new region, allocate a StringBuilder in the region, fill the builder with strings, and convert it into one string.

We can use regions to implement certain functional operations more efficiently. For example, here is a fast implementation of List.flatMap:

def flatMap(f: a -> List[b] \ ef, l: List[a]): List[b] \ ef =
    region rc {
        let ml = MutList.empty(rc);
        l |> List.forEach(x -> MutList.append(f(x), ml));
        MutList.toList(ml)
    }

Regions are Values

A region (or region handle) is a value that can be passed as a function argument. This is useful, for example, when we want to write a reusable function that allocates and returns a mutable data structure.

For example, here is the List.toMutDeque function:

def toMutDeque(rc: Region[r], l: List[a]): MutDeque[a, r] \ r =
    let d = MutDeque.empty(rc);
    foreach (x <- l) {
        MutDeque.pushBack(x, d)
    };
    d

The function takes a region handle rc, allocates a new mutable deque (MutDeq) in the given region, inserts all elements of the list l in the deque, and returns it.

Regions are Scoped

Regions and all memory associated with them cannot outlive their lexical scope.

Consider the following program:

def main(): Unit \ IO =
    let escaped = region rc {
        Array#{1, 2, 3} @ rc
    };
    println(escaped)

Here we allocate the Array#{1, 2, 3} in the region rc and try to return it outside of its enclosing scope. The Flix compiler detects such escape violations and reports an error:

❌ -- Type Error ----------------------------

>> The region variable 'rc' escapes its scope.

2 |>     let escaped = region rc {
3 |>         Array#{1, 2, 3} @ rc
4 |>     };

region variable escapes.

References

Flix supports mutable scoped references. A reference is a box whose value can change over time. The three key reference operations are:

• Creating a new reference Ref.fresh(rc, e).
• Dereferencing a reference Ref.get(e).
• Assigning to a reference Ref.put(e, e).

In Flix, the type of a reference is Ref[t, r] where t is the type of the element and r is its region. Like all mutable memory in Flix, every reference must belong to some region. Reading from and writing to a reference are effectful operations. For example, reading the value of a reference Ref[t, r] has effect r.

The Ref.fresh(rc, e) operation allocates a reference cell in a region of the heap and returns its location, the Ref.get operation dereferences a location and returns the content of a reference cell, and the assignment Ref.put operation changes the value of a reference cell. Informally, a reference cell can be thought of as an “object” with a single field that can be changed.

Allocating References

A reference cell is allocated with the Ref.fresh(rc, e) function. For example:

region rc {
    let c = Ref.fresh(rc, 42);
    println(Ref.get(c))
}

Here we introduce a region named rc. Inside the region, we create a reference cell called c with the value 42 which we then dereference and print.

Dereferencing References

A reference cell is accessed (dereferenced) with the Ref.get function. For example:

region rc {
    let c = Ref.fresh(rc, 42);
    let x = Ref.get(c);
    let y = Ref.get(c);
    println(x + y)
}

Here the program prints 42 + 42 = 84.

Assignment

We can update the value of a reference cell. For example:

region rc {
    let c = Ref.fresh(rc, 0);
    Ref.put(Ref.get(c) + 1, c);
    Ref.put(Ref.get(c) + 1, c);
    Ref.put(Ref.get(c) + 1, c);
    println(Ref.get(c))
}

Here the program creates a reference cell c with the value 0. We dereference the cell and increment its value three times. Hence the program prints 3.

Example: A Simple Counter

We can use references to implement a simple counter:

enum Counter[r: Region] { // The Region here is a type-kind
    case Counter(Ref[Int32, r])
}

def newCounter(rc: Region[r]): Counter[r] \ r = Counter.Counter(Ref.fresh(rc, 0))

def getCount(c: Counter[r]): Int32 \ r =
    let Counter.Counter(l) = c;
    Ref.get(l)

def increment(c: Counter[r]): Unit \ r =
    let Counter.Counter(l) = c;
    Ref.put(Ref.get(l) + 1, l)

def main(): Unit \ IO =
    region rc {
        let c = newCounter(rc);
        increment(c);
        increment(c);
        increment(c);
        getCount(c) |> println
    }

Here the Counter data type has a region type parameter. This is required since the counter internally uses a reference that requires a region. Hence Counters are also scoped. Note that the newCounter function requires a region handle to create a new Counter. Moreover, note that the functions getCount and increment both have the r effect.

Aliasing and References to References

References naturally support aliasing since that is their purpose. For example:

region rc {
    let l1 = Ref.fresh(rc, 42);
    let l2 = l1;
    Ref.put(84, l2);
    println(Ref.get(l1))
}

Prints 84 because the reference cell that l1 points to is modified through the alias l2.

References can also point to references as the following example illustrates:

region rc {
    let l1 = Ref.fresh(rc, 42);
    let l2 = Ref.fresh(rc, l1);
    let rs = Ref.get(Ref.get(l2));
    println(rs)
}

Here the type of l2 is Ref[Ref[Int32, rc], rc].

Mutable Tuples and Records

Flix tuples and records are immutable. However, tuples and records may contain mutable references.

For example, here is a pair that contains two mutable references:

region rc {
    let p = (Ref.fresh(rc, 1), Ref.fresh(rc, 2));
    Ref.put(123, fst(p))
};

The type of the pair is (Ref[Int32, rc], Ref[Int32, rc]). The assignment does not change the pair but instead changes the value of the reference cell in the first component.

Similarly, here is a record that contains two mutable references:

region rc {
    let r = { fstName = Ref.fresh(rc, "Lucky"), lstName = Ref.fresh(rc, "Luke") };
    Ref.put("Unlucky", r#fstName)
};

The type of the record is { fstName = Ref[String, rc], lstName = Ref[String, rc] }. Again, the assignment does not change the record, but instead changes the value of the reference cell corresponding to the fstName label.

Arrays

Flix supports mutable scoped arrays. An array is a fixed-length mutable sequence of elements that share the same type. Arrays are laid out consecutively in memory. Arrays are mutable; hence their elements can change over time. However, once created, the length of an array cannot be changed.

In Flix, the type of an array is Array[t, r] where t is the type of its elements and r is its region. Like all mutable memory in Flix, every array must belong to some region. Reading from and writing to arrays are effectful operations. For example, reading an element from an array of type Array[t, r] has the effect r. Likewise, creating an array in a region is also an effectful operation.

Arrays are always unboxed. For example, an array of type Array[Int32, r] is represented as a sequence of primitive 32-bit integers, i.e., in JVM terminology, the array is represented as int[]. Flix will never box primitive integers as java.lang.Integer objects but still permits primitives in generic collections and functions. The same is true for other types of primitives and arrays of primitives.

Arrays are low-level data structures typically used to implement higher-level data structures. Therefore, unless implementing such data structures, we recommend that arrays are used sparingly. Instead, we recommend using the MutList, MutDeque, MutSet, and MutMap data structures.

Hint: Use MutList if you need a growable mutable sequence of elements.

Array Literals

The syntax of an array literal is of the form Array#{e1, e2, e3, ...} @ r where e1, e2, and so forth are element expressions, and r is the region expression. For example:

region rc {
    let fruits = Array#{"Apple", "Pear", "Mango"} @ rc;
    println(Array.toString(fruits))
}

Here we introduce a region named rc. Inside the region, we create an array of fruits that contain the three strings "Apple", "Pear", and "Mango". The type of fruits is Array[String, rc]. For more information about regions, we refer to the chapter on Regions.

Running the program prints Array#{"Apple", "Pear", "Mango"}.

Allocating Arrays

We can allocate an array of size n filled with the same element using the Array.repeat function. For example:

region rc {
    let arr = Array.repeat(rc, 1_000, 42);
    println(Array.toString(arr))
}

Here we create an array arr of length 1_000 where each array element has the value 42. Note that we must pass the region rc as an argument to Array.repeat because the function must know to which region the returned array should belong.

We can also create an array filled with all integers from zero to ninety-nine:

region rc {
    let arr = Array.range(rc, 0, 100);
    println(Array.toString(arr))
}

Moreover, we can convert most data structures to arrays. For example:

region rc {
    let fruitList = List#{"Apple", "Pear", "Mango"};
    let fruitArray = List.toArray(rc, fruitList);
}

Note that we must pass the region rc as an argument to List.toArray since the function must know to which region the returned array should belong.

Allocating Arrays with Uninitialized Elements

We can use the Array.empty function to create an array of a given length where the content of the array is uninitialized. For example:

region rc {
    let arr: Array[String, rc] = Array.empty(rc, 100);
    // ... initialize `arr` here ...
}

Here we create an array of length 100 of type Array[String, rc]. We use an explicit type annotation : Array[String, rc] to inform Flix of the expected type of the array.

Warning: It is dangerous to use arrays that have uninitialized elements.

What are the elements of an uninitialized array? Flix follows Java (and the JVM) which defines a default value for every primitive– and reference type. So, for example, the default values for Bool and Int32 are false and 0, respectively. The default value for reference types are null. So be careful! Flix does not have a null value, but one can be indirectly introduced by reading from improperly initialized arrays which can lead to NullPointerExceptions.

Reading from and Writing to Arrays

We can retrieve or update the element at a specific position in an array using Array.get and Array.put, respectively. For example:

region rc {
    let strings = Array.empty(rc, 2);
    Array.put("Hello", 0, strings);
    Array.put("World", 1, strings);
    let s1 = Array.get(0, strings);
    let s2 = Array.get(1, strings);
    println("${s1} ${s2}")
}

Here we create an empty array of length of two. We then store the string "Hello" at position zero and the string "World" at position one. Next, we retrieve the two strings, and print them. Thus the program, when compiled and run, prints Hello World.

We can also write part of the program in a more fluent-style using the !> pipeline operator:

let strings =
    Array.empty(rc, 2) !>
    Array.put("Hello", 0) !>
    Array.put("World", 1);

Slicing Arrays

We can slice arrays using Array.slice. A slice of an array is a new (shallow) copy of a sub-range of the original array. For example

region rc {
    let fruits = Array#{"Apple", "Pear", "Mango"} @ rc;
    let result = Array.slice(rc, start = 1, end = 2, fruits);
    println(Array.toString(result))
}

which prints Array#{"Pear"} when run.

Taking the Length of an Array

We can compute the length of an array using the Array.length function. For example

region rc {
    let fruits = Array#{"Apple", "Pear", "Mango"} @ rc;
    println(Array.length(fruits))
}

which prints 3 when run.

Note: We advise against indexed-based iteration through arrays. Instead, we recommend to use functions such as Array.count, Array.forEach, and Array.transform.

Additional Array Operations

The Array module offers an extensive collection of functions for working with arrays. For example, Array.append, Array.copyOfRange, Array.findLeft, Array.findRight, Array.sortWith, and Array.sortBy to name a few. In total, the module offers more than 100 functions ready for use.

Structs

Flix supports mutable scoped structs. A struct is a sequence of user-defined fields. Fields are immutable by default, but can be made mutable by marking them with the mut modifier. Like all mutable memory in Flix, every struct must belong to some region.

Structs are the mutable alternative to extensible records which are immutable.

The fields of a struct are unboxed, i.e. primitive types do not cause indirection. Thus structs are a memory efficient data structure that can be used to implement higher-level mutable data structures, e.g. mutable lists, mutable stacks, mutable queues, and so forth.

Flix supports three operations for working with structs:

• Creating a struct instance in a region with new Struct @ rc { ... }.
• Accessing a field of a struct with struct->field.
• Updating a mutable field of a struct with struct->field = ....

Each operation has an effect in the region of the struct.

Declaring a Struct

We can declare a struct as follows:

struct Person[r] {
    name: String,
    mut age: Int32,
    mut height: Int32
}

Here we declare a struct with three fields: name, age, and height. The name field is immutable, i.e. cannot be changed once the struct instance has been created. The age and heights are mutable and hence can be changed after creation. The Person struct has one type parameter: r which specifies the region that the struct belongs to.

Every struct must have a region type parameter and it must be the last in the type parameter list.

Creating a Struct

We can create an instance of the Person struct as follows:

mod Person {
    pub def mkLuckyLuke(rc: Region[r]): Person[r] \ r =
        new Person @ rc { name = "Lucky Luke", age = 30, height = 185 }
}

The mkLuckyLuke function takes one argument: the region capability rc to associate with the struct.

The syntax:

new Person @ rc { name = "Lucky Luke", age = 30, height = 185 }

specifies that we create a new instance of the Person struct in the region rc. We then specify the values of each field of the struct. All struct fields must be initialized immediately and explicitly.

Reading and Writing Fields

We can read and write fields of a struct using the field access operator ->. For example:

mod Person {
    pub def birthday(p: Person[r]): Unit \ r =
        p->age = p->age + 1;
        if(p->age < 18) {
            p->height = p->height + 10
        } else {
            ()
        }
}

The birthday function takes a Person struct p and mutates its age and height fields.

For example, in the line:

p->age = p->age + 1;

we access the current age as p->age, increment it, and store the result back in the age field.

We must distinguish between the struct field access operator -> and the function arrow   ->  . The former has no space around it, whereas the latter should have space on both sides. In summary:

• s->f: is a struct field access of field f on struct s.
• x -> x: is a function from formal parameter x to the variable expression x.

Field Visibility

In Flix, the fields of a struct are only visible from within its companion module. We can think of this as a form of compiler-enforced encapsulation.

For example, if we write:

struct Point[r] {
    x: Int32,
    y: Int32
}

def area(p: Point[r]): Int32 \ r = 
    p->x * p->y

The Flix compiler emits two errors:

❌ -- Resolution Error -------------------------------------------------- 

>> Undefined struct field 'x'.

7 |     p->x * p->y
           ^
           undefined field

❌ -- Resolution Error -------------------------------------------------- 

>> Undefined struct field 'y'.

7 |     p->x * p->y
                  ^
                  undefined field

Instead, we should define the area function inside the companion module:

struct Point[r] {
    x: Int32,
    y: Int32
}

mod Point { // Companion module for Point
    pub def area(p: Point[r]): Int32 \ r = 
        p->x * p->y
}

If we want to provide access to the fields of a struct from outside its companion module, we can introduce explicit getters and setters. For example:

mod Point {
    pub def getX(p: Point[r]): Int32 \ r = p->x
    pub def getY(p: Point[r]): Int32 \ r = p->y
}

Thus access to the fields of struct is tightly controlled.

Immutable and Mutable Fields

In Flix, every field of a struct is either immutable or mutable. A mutable field must be marked with the mut modifier. Otherwise the field is immutable by default, i.e. the value of the field cannot be changed once the struct instance has been created.

For example, we can define a struct to represent a user:

struct User[r] {
    id: Int32,
    mut name: String,
    mut email: String
}

Here the identifier id is immutable and cannot be changed whereas the name and email fields can be changed over the lifetime of the struct instance.

If we try to modify an immutable field:

mod User {
    pub def changeId(u: User[r]): Unit \ r =
        u->id = 0
}

The Flix compiler emits an error:

❌ -- Resolution Error -------------------------------------------------- 

>> Modification of immutable field 'id' on User'.

9 |         u->id = 0
               ^^
               immutable field

Mark the field as 'mut' in the declaration of the struct.

We remark that field immutability is not transitive.

For example, we can define a struct:

struct Book[r] {
    title: String,
    authors: MutList[String, r]
}

where the authors field is immutable.

However, since a MutList can be changed, we can write:

mod Book {
    pub def addAuthor(a: String, b: Book[r]): Unit \ r =
        MutList.push(a, b->authors)
}

Here we are not changing the field of the struct. We are changing the underlying mutable list.

Recursive and Polymorphic Structs

We can define a struct for a binary search tree that is recursive and polymorphic:

struct Tree[k, v, r] {
    key: k,
    mut value: v,
    mut left: Option[Tree[k, v, r]],
    mut right: Option[Tree[k, v, r]]
}

If we assume that Tree[k, v, r] is sorted, we can define a search function:

mod Tree {
    // A function to search the tree `t` for the given key `k`.
    pub def search(k: k, t: Tree[k, v, r]): Option[v] \ r with Order[k] =
        match (Order.compare(k, t->key)) {
            case Comparison.EqualTo  => Some(t->value)
            case Comparison.LessThan =>
                // Search in the left subtree.
                match t->left {
                    case None            => None
                    case Some(leftTree)  => search(k, leftTree)
                }
            case Comparison.GreaterThan =>
                // Search in the right subtree.
                match t->right {
                    case None            => None
                    case Some(rightTree) => search(k, rightTree)
                }
        }
}

Mutable Collections

The Flix standard library supports many immutable collections, including options, lists, chains, sets, and maps. We strongly encourage their use.

In addition, the Flix standard library also offers several mutable collections:

• MutList[t, r] : a contiguous growable/shrinkable array of elements of type t.
• MutSet[t, r] : a mutable set of elements of type t.
• MutMap[k, v, r] : a mutable map of keys of type k to values of type v.
• MutDeque[t, r] : a mutable double-ended queue of elements of type t.

Recall that in Flix all mutable memory, including mutable collections, belongs to a region.

Here is an example of how to use MutList[t]:

def main(): Unit \ IO =
    region rc {
        let fruits = MutList.empty(rc);
        MutList.push("Apple", fruits);
        MutList.push("Pear", fruits);
        MutList.push("Mango", fruits);
        MutList.forEach(println, fruits)
    }

which prints Apple, Pear, and Mango. Here the MutList[String, rc] automatically expands (and shrinks) as elements are pushed (or popped) from it.

We can write the above program in a more fluent-style using the !> pipeline operator:

def main(): Unit \ IO =
    region rc {
        let fruits =
            MutList.empty(rc) !>
            MutList.push("Apple") !>
            MutList.push("Pear") !>
            MutList.push("Mango");
        MutList.forEach(println, fruits)
    }

We can split the above program into several functions as follows:

def main(): Unit \ IO =
    region rc {
        let fruits = sweetFruits(rc);
        printFruits(fruits)
    }

def sweetFruits(rc: Region[r]): MutList[String, r] \ r =
    MutList.empty(rc) !>
    MutList.push("Apple") !>
    MutList.push("Pear") !>
    MutList.push("Mango")

def printFruits(fruits: MutList[String, r]): Unit \ {r, IO} =
    MutList.forEach(println, fruits)

Here the main function introduces a new region rc. We pass this region to sweetFruits which creates and returns a new mutable list of fruits. Note that sweetFruits has the effect r since it allocates mutable memory using rc. The printFruits takes a mutable list of fruits and prints them. Note that this function has effect r since it reads from mutable memory in r and it has effect IO since it prints to the terminal.

Control Structures

Flix — being a functional programming language — has few control-structures. Most control is simply function application. The Flix control structures are:

• If-Then-Else: A traditional if-then-else expression.
• Pattern Matching: A functional construct for taking apart algebraic data types.
• Foreach: An imperative construct for iteration through collections.
• Monadic For-Yield: A functional construct for monadic operations, similar to Scala’s for-comprehensions and Haskell’s do-notation.
• Applicative For-Yield: A functional construct for applicative operations, similar to Haskell’s applicative do-notation.

What’s the difference between foreach, monadic forM, and applicative forA?:

The following table gives some uses cases for each construct:

Note: Flix does not have traditional while or for-loops. Instead, we recommend the use of recursion and/or one of the above constructs.

If-then-else

Flix supports the usual if-then-else expression:

if (1 == 1) "Hello" else "World"

which evaluates to Hello.

But if guards are also supported in other parts of the language.

Guarded Pattern Matches

We can use an if-guard in a pattern match:

def isSquare(s: Shape): Bool = match s {
    case Rectangle(h, w) if h == w => true
    case _                         => false
}

Guarded Datalog Rules

We can use an if-guard in a Datalog rule:

Path(x, z) :- Path(x, y), Edge(y, z), if (x != z).

Note that the parentheses around the guard are mandatory.

Pattern Matching

Matching on Enums

Flix supports pattern matching on algebraic data types.

For example, if we have an algebraic data type that models shapes:

enum Shape {
    case Circle(Int32)
    case Square(Int32)
    case Rectangle(Int32, Int32)
}

Then we can write a function to compute the area of a Shape using pattern matching:

def area(s: Shape): Int32 = match s {
    case Shape.Circle(r)       => 3 * (r * r)
    case Shape.Square(w)       => w * w
    case Shape.Rectangle(h, w) => h * w
}

Matching on Records

The above also works for record types; however, the syntax is slightly different. Let us rewrite the Shape type from before, this time using records.

enum Shape {
    case Circle({ radius = Int32 })
    case Square({ width = Int32 })
    case Rectangle({ height = Int32, width = Int32 })
}

def area(s: Shape): Int32 = match s {
    case Shape.Circle({ radius })           => 3 * (radius * radius)
    case Shape.Square({ width })            => width * width
    case Shape.Rectangle({ height, width }) => height * width
}

In the example above, we implicitly require that each pattern has exactly the specified labels. No more, no less. However, in general, the syntax for record patterns is similar to their types. Thus, we can match on a record that has at least one specific label.

def f(r: { height = Int32 | a }): Int32 = match r {
    case { height | _ } => height
    // The extension has a wildcard pattern since it is unused
}

Note, however, that the pattern also implies a type, thus the following example will not work.

def badTypes(r: { height = Int32 | a }): Int32 = match r {
    case { height } => height
}

Additionally, all cases must have the same type, so this will also not work:

match ??? {
    case { height | _ } => height
    case { height }     => height
}

This may be a contrived example, but it demonstrates a common pitfall, which is easily fixed.

This is because the first case is a polymorphic record with a defined height-label, whereas the second case matches on a closed record that only has the height-label defined.

Additionally, the { label } pattern is actually syntactic sugar for { label = pattern }. Thus, if you are dealing with multiple records, then it may be necessary to use different patterns.

def shadowing(r1: { height = Int32 | a }, r2: { height = Int32 | b }): Int32 =
    match (r1, r2) {
        case ({ height | _ }, { height | _ }) => height + height
        // This does not work because `height = height` is defined twice
    }

However, renaming the variables makes the program type check.

def renaming(r1: { height = Int32 | a }, r2: { height = Int32 | b }): Int32 =
    match (r1, r2) {
        case ({ height = h1 | _ }, { height = h2 | _ }) => h1 + h2
    }

To summarize, here are a few examples of record patterns:

• { } - the empty record
• { radius = r } - a record containg only the label radius where the value is bound to r in the scope
• { radius } - a record containing only the label radius (this is actually syntactic sugar for { radius = radius })
• { radius | _ } - a record containg at least the label radius
• { radius | r } - a record containg at least the label radius where the rest of the record is bound to r

Let Pattern Match

In addition to the pattern match construct, a let-binding can be used to destruct a value. For example:

let (x, y, z) = (1, 2, 3)

Binds the variables x, y, and z to the values 1, 2, and 3, respectively.

Any exhaustive pattern may be used in a let-binding. For example:

let (x, Foo(y, z)) = (1, Foo(2, 3))

is legal provided that the Foo constructor belongs to a type where it is the only constructor.

The following let-bindings are illegal because they are not exhaustive:

let (1, 2, z) = ...
let Some(x) = ...

The Flix compiler will reject such non-exhaustive patterns.

Let-pattern-matches work well with records, as they allow you to destructure a record and only use the labels you are interested in:

let { height | _ } = r;
height + height

Match Lambdas

Pattern matches can also be used with lambda expressions. For example:

List.map(match (x, y) -> x + y, (1, 1) :: (2, 2) :: Nil)

is equivalent to:

List.map(w -> match w { case (x, y) => x + y }, (1, 1) :: (2, 2) :: Nil)

As for let-bindings, such pattern matches must be exhaustive.

Note the difference between the two lambda expressions:

let f = (x, y, z) -> x + y + z + 42i32
let g = match (x, y, z) -> x + y + z + 42i32

Here f is a function that expects three Int32 arguments, whereas g is a function that expects one three tuple (Int32, Int32, Int32) argument.

Foreach

Flix supports a traditional foreach construct that enables imperative iteration through collections.

We typically use the foreach construct when we want to iterate through one or more collections and execute an effectful operation for each of their elements.

For example, the program:

def main(): Unit \ IO = 
    let fruits = List#{"Apple", "Pear", "Mango"};
    foreach (fruit <- fruits) 
        println(fruit)

Prints the strings Apple, Pear, and Mango.

We can also iterate through multiple collections:

def main(): Unit \ IO = 
    let fruits = List#{"Apple", "Pear", "Mango"};
    let creams = List#{"Vanilla", "Stracciatella"};
    foreach (fruit <- fruits) 
        foreach (cream <- creams)
            println("Would you like some ${fruit} with ${cream} icecream?")

The same loop can also be written:

def main(): Unit \ IO = 
    let fruits = List#{"Apple", "Pear", "Mango"};
    let creams = List#{"Vanilla", "Stracciatella"};
    foreach (fruit <- fruits; cream <- creams) 
        println("Would you like some ${fruit} with ${cream} icecream?")

We can also write loops with a filter. For example:

def main(): Unit \ IO = 
    let fruits = List#{"Apple", "Pear", "Mango"};
    let creams = List#{"Vanilla", "Stracciatella"};
    foreach (fruit <- fruits; if isExcotic(fruit); cream <- creams) 
        println("Would you like some ${fruit} with ${cream} icecream?")

def isExcotic(fruit: String): Bool = match fruit {
    case "Mango" => true
    case _       => false
}

Adding Optional Braces for Visual Clarity

We can sometimes improve the visual clarity of a foreach expression by adding braces:

def main(): Unit \ IO = 
    let fruits = List#{"Apple", "Pear", "Mango"};
    let creams = List#{"Vanilla", "Stracciatella"};
    foreach (fruit <- fruits) {
        foreach (cream <- creams) {
            println("Would you like some ${fruit} with ${cream} icecream?")
        }
    }

The braces have no impact on the meaning of the foreach loop; they are purely stylistic.

The ForEach Trait

We can use the foreach syntax to iterate through any collection type that implements the ForEach trait. In particular, the ForEach trait defines a single signature:

///
/// A trait for data structures that support a forEach operation.
///
trait ForEach[t] {

    ///
    /// The type of elements in the data structure.
    ///
    type Elm: Type

    ///
    /// The effect of `forEach`.
    ///
    type Aef: Eff = {}

    ///
    /// Applies `f` to each element in the data structure.
    ///
    pub def forEach(f: ForEach.Elm[t] -> Unit \ ef, t: t): Unit \ (ef + ForEach.Aef[t])

}

Note: Flix expects the expression body of a foreach to have type Unit.

ForEach Combinators

The ForEach module provides four combinators that transform how a collection is iterated: withIndex, withFilter, withMap, and withZip. Each combinator wraps a collection and returns a new ForEach-compatible value that can be used directly with the foreach syntax.

Iterating with an Index

The withIndex combinator pairs each element with its zero-based index:

use ForEach.withIndex;
def main(): Unit \ IO =
    let langs = List#{"Flix", "Haskell", "Scala"};
    foreach ((i, lang) <- withIndex(langs)) {
        println("${i}: ${lang}")
    }

This prints:

0: Flix
1: Haskell
2: Scala

Filtering Elements

The withFilter combinator skips elements that do not satisfy a predicate:

use ForEach.withFilter;
def main(): Unit \ IO =
    let numbers = List#{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    foreach (x <- withFilter(x -> x `Int32.modulo` 2 == 0, numbers)) {
        println("${x}")
    }

This prints only the even numbers: 2, 4, 6, 8, 10.

Mapping Elements

The withMap combinator applies a transformation to each element before it is yielded:

use ForEach.withMap;
def main(): Unit \ IO =
    let numbers = List#{1, 2, 3, 4, 5};
    foreach (x <- withMap(x -> x * 10, numbers)) {
        println("${x}")
    }

This prints 10, 20, 30, 40, 50.

Zipping Two Collections

The withZip combinator zips two collections element-wise, producing pairs. The iteration stops when the shorter collection is exhausted:

use ForEach.withZip;
def main(): Unit \ IO =
    let names = List#{"Alice", "Bob", "Carol"};
    let ages = List#{30, 25, 40};
    foreach ((name, age) <- withZip(names, ages)) {
        println("${name} is ${age} years old")
    }

Note: withZip requires both collections to implement the Iterable trait (not just ForEach).

Monadic For-Yield

Flix supports a monadic forM-yield construct similar to Scala’s for-comprehensions and Haskell’s do notation. The forM construct is syntactic sugar for uses of point and flatMap (which are provided by the Monad trait). The forM construct also supports a guard-expression that uses empty (which is provided by the MonadZero trait).

For example, the monadic forM expression:

let l1 = 1 :: 2 :: Nil;
let l2 = 1 :: 2 :: Nil;
forM (x <- l1; y <- l2)
    yield (x, y)

evaluates to the list:

(1, 1) :: (1, 2) :: (2, 1) :: (2, 2) :: Nil

Using Guard Expressions

We can use guard expressions in forM expressions. For example, the program:

let l1 = 1 :: 2 :: Nil;
let l2 = 1 :: 2 :: Nil;
forM (x <- l1; y <- l2; if x < y)
    yield (x, y)

evaluates to the list:

(1, 2) :: Nil

Working with Options and Results

We can also use forM to work with the Option data type. For example:

def divide(x: Int32, y: Int32): Option[Int32] = 
    if (y == 0) None else Some(x / y)

def f(): Option[Int32] = 
    forM (
        x <- divide(5, 2);
        y <- divide(x, 8);
        z <- divide(9, y)
    ) yield x + y + z

Here the function f returns None since x = 5 / 2 = 2 and 2 / 8 = 0 hence the last division fails.

Similarly, we can use forM to work with the Result[e, t] data type. For example:

use Sys.Console

def main(): Result[String, Unit] \ IO =
    println("Please enter your first name, last name, and age:");
    forM (
        fstName <- Console.readln();
        lstName <- Console.readln();
        ageLine <- Console.readln();
        ageNum  <- Int32.parse(10, ageLine)
    ) yield {
        println("Hello ${lstName}, ${fstName}.");
        println("You are ${ageNum} years old!")
    }

Here main prompts the user to enter their first name, last name, and age. Each call to Console.readln returns a Result[String, String] value which is either an error or the input string. Thus the local variables fstName, lstName, and ageLine are Strings. We parse ageLine into an Int32 using Int32.parse, which returns a Result[String, Int32] value. If every operation is successful then we print a greeting and return Ok(()) (i.e., Ok of Unit). Otherwise, we return an Err(msg) value.

Working with Other Monads

We can use forM with other types of Monads, including Chain and Nels (non-empty lists). For example, we can write:

let l1 = Nel(1, 2 :: Nil);
let l2 = Nel(1, 2 :: Nil);
forM (x <- l1; y <- l2)
    yield (x, y)

which evaluates to the non-empty list:

Nel((1, 1), (1, 2) :: (2, 1) :: (2, 2) :: Nil)

Note: We cannot use an if-guard with non-empty lists because such an if-guard requires an instance of the MonadZero trait which is not implemented by non-empty list (since such a list cannot be empty).

Desugaring

The forM expression is syntactic sugar for uses of Monad.flatMap, Applicative.point, and MonadZero.empty.

For example, the expression:

let l1 = 1 :: 2 :: Nil;
let l2 = 1 :: 2 :: Nil;
forM (x <- l1; y <- l2; if x < y)
    yield (x, y)

is de-sugared to:

Monad.flatMap(x -> 
    Monad.flatMap(y -> 
        if (x < y)
            Applicative.point((x, y))
        else 
            MonadZero.empty(), 
    l2), 
l1);

Applicative For-Yield

In addition to the monadic forM expression, Flix supports an applicative forA expression that builds on the Applicative trait. The forA construct makes it simple to write error-handling code which uses the Validation[e, t] data type.

Working with Validations

We can use the forA expression to validate user input while collecting all errors.

enum Connection(String, String)

enum InvalidInput {
    case InvalidUserName,
    case InvalidPassword
}

def validateUser(s: String): Validation[InvalidInput, String] =
    if (8 <= String.length(s) and String.forAll(Char.isLetter, s))
        Validation.Success(s)
    else 
        Validation.Failure(Nec.singleton(InvalidInput.InvalidUserName))

def validatePass(s: String): Validation[InvalidInput, String] =
    if (12 <= String.length(s) and String.length(s) <= 20)
        Validation.Success(s)
    else 
        Validation.Failure(Nec.singleton(InvalidInput.InvalidPassword))

def connect(u: String, p: String): Validation[InvalidInput, Connection] = 
    forA (
        user <- validateUser(u);
        pass <- validatePass(p)
    ) yield Connection.Connection(user, pass)

The expression:

connect("Lucky Luke", "Ratata")

evaluates to:

Failure(Nec#{InvalidUserName, InvalidPassword})

which contains both input validation errors. On the other hand, the expression:

connect("luckyluke", "password12356789")

evaluates to:

Success(Connection(luckyluke, password12356789))

Applicatives are Independent Computations

We can write a monadic forM expression where the result of one monadic operation is used as the input to another monadic operation. For example:

forM(x <- Some(123);  y <- Some(x)) 
    yield (x, y)

Here the value of y depends on x. That is, the computation of x and y are not independent.

If we try to same with the applicative forA expression:

forA(x <- Some(123); y <- Some(x))
    yield (x, y)

then the Flix compiler emits a compiler error:

❌ -- Resolution Error --------------

>> Undefined name 'x'.

10 |         y <- Some(x)
                       ^
                       name not found

because the computations of x and y are independent and hence the value of x is not in scope when we define the value of y.

Desugaring

The forA expression is syntactic sugar for uses of Functor.map and Applicative.ap.

For example, the expression:

let o1 = Some(21);
let o2 = Some(42);
forA(x <- o1; y <- o2) 
    yield x + y;

is de-sugared to:

Applicative.ap(Functor.map(x -> y -> x + y, o1), o2)

Effect System

Flix features a state-of-the-art type and effect system fully integrated into the language. The Flix effect system is powerful and extensive, supporting effect polymorphism, sub-effecting, effect exclusion, purity reflection, and associated effects.

We will explore these new and exciting features over the coming pages.

What are the benefits of an effect system? There are many:

• (Purity) A type and effect system separates pure and impure functions. In Flix, a pure function cannot have any side-effects and must return the same value when given the same arguments. Nevertheless, a pure function can still be implemented in an imperative style using mutable data structures as long as those data structures leave scope when the function ends.

• (Reasoning) A type and effect system helps programmers understand how their programs work by requiring every function to specify its argument and return types, as well as the side-effects of the function.

• (Modularity) A type and effect system enforces modularity by forcing programmers to consider what side effects are allowed where in the program. Moreover, effects — like types — serve as compiler checked documentation.

• (Effects and Handlers) A type and effect system is the foundation for algebraic effects and handlers. These allow programmers to implement their own control structures, such as exceptions, async/await, and cooperative multitasking.

• (Security) A type and effect system offers iron-clad guarantees about the behavior of functions, allowing programmers to increase their trust in unknown code. For example, if a function is pure, it cannot have any side-effects: it cannot access the file system, the network, etc. A specific benefit is that programs become more resistant to supply chain attacks.

• (Purity Reflection) The Flix Standard Library (and other library authors in extension) can use purity reflection to inspect the purity of function arguments passed to higher-order functions. We can exploit this information to implement automatic parallelization while preserving the original semantics of the program. For example, in Flix, the Set.count function uses parallel evaluation if (a) the set is sufficiently large and (b) the passed predicate function is pure.

• (Optimizations) The Flix compiler exploits purity information for aggressive dead code elimination and inlining.

The Flix type and effect system is quite sophisticated and requires some background knowledge to use effectively. In the next couple of sections, we gradually introduce the features of the type and effect system and give several examples of its use.

Before we continue, it is important to understand that Flix has three types of effects:

• primitive effects
• algebraic effects
• heap effects

We describe how traits and effects interact in the section on Associated Effects.

Direct Style

Flix is a so-called direct-style programming language with a traditional type and effect system. This is in contrast to so-called functional effect systems like Cats Effect, Kyo, and ZIO. These systems offer a library-level effect system, essentially a custom IO monad. While this approach has some advantages, the downsides are at least twofold (a) we do not get any of the guarantees offered by a traditional type and effect system (e.g., we cannot know when a function is pure), and (b) we must write our program in a monadic-style, which is burdensome.

Primitive Effects

Note: This page is slightly updated and pending a rewrite.

Flix comes with a collection of pre-defined primitive effects. Unlike algebraic and heap effects, primitive effects cannot be handled and never go out of scope. A primitive effect represents a side-effect that happens on the machine. It cannot be undone or reinterpreted.

The most important primitive effect is the IO effect.

The IO Effect

The IO effect represents any action that interacts with the world outside the program. Such actions include printing to the console, creating, reading, and writing files, accessing the network, and more. The IO represents actions that change the outside world (e.g., modifying a file) but also actions that merely access the outside world (e.g., retrieving the current time). Unlike a pure function, a function with the IO effect may change behavior every time it is called, even if its arguments are the same. For example, reading the same file twice is not guaranteed to return the same result since the file may have changed between the two accesses.

The IO effect, and all other primitive effects, are viral. If a function has a primitive effect, all its callers will also have that primitive effect. That is to say, once you have tainted yourself with impurity, you remain tainted.

The Other Primitive Effects

• NonDet: The NonDet effect represents an almost pure computation. For example, a function that flips a coin is virtually pure; it has no side-effects. Yet, it may return different results, even when given the same arguments.

Effect Polymorphism

In Flix, we can express that a function is pure (i.e. has no side-effects):

def inc(x: Int32): Int32 \ { } = x + 1
                        // ^^^ empty effect set

The inc function is pure because its effect set is empty. When a function is pure, we know that the function must return the same value when given the same arguments. Moreover, the function cannot have any side-effect on the outside world.

We do not have to write the empty effect set. We can simply write:

def inc(x: Int32): Int32 = x + 1

In Flix, we can express that a function has a single effect:

def incAndPrint(x: Int32): Int32 \ {IO} = 
    let result = x + 1;         // ^^^^ singleton effect set
    println(result);
    result

Here the incAndPrint function has the primitive IO effect.

We can also express that a function has multiple effects:

def copyFile(src: File, dst: File): Unit \ {FsRead, FsWrite, IO} = ...
                                         // ^^^^^^^^^^^^^^^^^^^^ multiple effects

Here the copyFile function has three primitive effects: FsRead, FsWrite, and IO.

In Flix, we can express a function that has a heap effect:

def nth(i: Int32, a: Array[t, r]): Option[a] \ {r} = ....
                                            // ^^^ heap effect

Here the nth function has a heap effect in the region r.

We can also write functions that mix different effects:

use Time.Clock

def strange(a: Array[t, r]): Unit \ {r, Clock, Http, IO}
                                 // ^^^^^^^^^^^^^^^^^^^ a mixture of effects

This function has a heap effect r and three effects: Clock, Http, and IO.

Higher-Order Functions

When we write higher-order functions, we must think carefully about their effect behavior.

For example, we can write a higher-order function Set.exists:

def exists(f: a -> Bool \ { }, s: Set[a]): Bool = ...
                          ^^^

Here the exists function enforces the predicate function f to be pure. Why would we do this? For at least two reasons: (a) it allows us to hide the iteration order used in the set, and (b) it allows us to perform the counting in parallel.

Nevertheless, requiring a function to be pure unless necessary is considered a bad programming style. Instead, we should write effect polymorphic functions. An effect polymorphic function is a higher-order function whose effects depend on the effects of its function arguments.

For example, we can write an effect polymorphic map function:

def map(f: a -> b \ ef, l: List[a]): List[b] \ ef = ...
                    ^^ // effect variable      ^^ effect variable

The type and effect signature of map states: If map is given a function f with effects ef then calling map has the effects ef. That is, if f is pure (i.e. has no effects) then the call to map will be pure. If f has the IO effect then the call to map will have the IO effect:

List.map(x -> x + 1, l)               // has the { } effect (i.e., is pure)
List.map(x -> {println(x); x + 1}, l) // has the { IO } effect

A higher-order function that takes multiple function arguments may combine their effects.

For example, the Flix Standard Library definition of forward function composition >>takes two functions f and g, and composes them:

def >>(f: a -> b \ ef1, g: b -> c \ ef2): a -> c \ (ef1 + ef2) = x -> g(f(x))

The type and effect signature of >> states: If map is given two functions f with effects ef1 and g with effects ef2 then it returns a new function which has the union of effects ef1 + ef2.

In Flix, the language of effects is based on set formulas:

• The complement of ef is written ~ef.
• The union of ef1 and ef2 is written ef1 + ef2.
• The intersection of ef1 and ef2 is written ef1 & ef2.
• The difference of ef1 and ef2 is written ef1 - ef2.

By far the most common operation is to compute the union of effects.

It’s important to understand that there can be several ways to write the same effect set. For example, ef1 + ef2 is equivalent to ef2 + ef1, as one would expect.

Effect Exclusion

A novel feature of Flix is its support for effect exclusion. In simple terms, effect exclusion allows us to write higher-order functions that disallow specific effects while allowing all other effects.

For example, we can write an event listener registration function:

def onClick(listener: KeyEvent -> Unit \ (ef - Block), ...): ... 

Here the onClick function takes an event listener that may have any effect, except the Block effect. Hence listener can perform any action, except for an action that would block the UI thread.

As another example, we can write an exception handler function:

def recoverWith(f: Unit -> a \ Throw, h: ErrMsg -> a \ (ef - Throw)): a = ... 

Here the recoverWith function takes two function arguments: the function f that may throw an exception and a handler h which can handle the error. Notably, the effect system enforces that h cannot itself throw an exception.

Sub-Effecting

Note: This feature is not yet enabled.

Flix supports sub-effecting which allows an expression or a function to widen its effect set.

For example, if we write:

if (???) { x -> x + 1 } else { x -> {println(x); x + 1}}

The first branch should have type Int32 -> Int32 \ { } (i.e. it is pure) whereas the second branch has type Int32 -> Int32 \ { IO }. Without sub-effecting these two types are incompatible because { } != { IO }. However, because of sub-effecting, Flix gives the first branch the type Int32 -> Int32 \ ef for some fresh effect variable ef. This allows type inference to widen the effect of the first branch to IO. Hence the compiler is able to type check the whole expression.

As another example:

def handle(f: Unit -> a \ (ef + Throw)): a = ...

Here the handle function expects a function argument f with the Throw effect. However, due to sub-effecting, we can still call the handle function with a pure function, i.e.:

def handle(x -> Throw.throw(x))    // OK, has the `Throw` effect.
def handle(x -> x)                 // OK, because of sub-effecting.
def handle(x -> println(x))        // Not OK, handle does not permit `IO`.

Flix also allows sub-effect in instance declarations.

For example, we can define the trait:

trait Foo[t] {
    def f(x: t): Bool \ { IO }
}

where f has the IO effect. We can implement it:

instance Foo[Int32] {
    def f(x: Int32): Bool = x == 0 // Pure function
}

The declared effect of f is IO, but here the implementation of f is pure (i.e., it has the empty effect set { }). The program still type checks because { } can be widened to IO.

Flix, however, does not allow sub-effecting for top-level functions.

For example, if we declare the function:

def foo(): Bool \ IO = true

The Flix compiler emits the error message:

❌ -- Type Error ------------------------------

>> Expected type: 'IO' but found type: 'Pure'.

1 | def foo(): Bool \ IO = true
    ^^^^^^^^^^^^^^^^^^^^^^^^^^^
    expression has unexpected type.

In summary, Flix allows effect widening in two cases: for (a) lambda expressions and (b) instance definitions. We say that Flix supports abstraction site sub-effecting and instance definition sub-effecting.

Effects and Handlers

Flix supports algebraic effects and handlers in the style of Eff and Koka.

Flix effect handlers use dynamic scope, deep handlers, and support multiple resumptions.

In this section, we introduce effects and handlers, but we also recommend the reader take a look at:

• An Introduction to Algebraic Effects and Handlers — Matija Pretnar

We begin a type of effect most programmers are familiar with: exceptions.

Non-Resumable Effects: Exceptions

We can use effects and handlers to implement exceptions. For example:

eff DivByZero {
    def divByZero(): Void
}

def divide(x: Int32, y: Int32): Int32 \ DivByZero = 
    if (y == 0) {
        DivByZero.divByZero()
    } else {
        x / y
    }

def main(): Unit \ IO = 
    run {
        println(divide(3, 2));
        println(divide(3, 0))
    } with handler DivByZero {
        def divByZero(_resume) = println("Oops: Division by Zero!")
    }

Here we declare the effect DivByZero and use it inside the divide function. Hence the divide function has the DivByZero effect. In main we perform two divisions. The first succeeds and prints 1. The second fails and prints an error message. The continuation, _resume, is unused and cannot be used because its argument type is Void. The main function has the IO effect since we use println in the handler, but it does not have the DivByZero effect since that has been handled.

Exceptions are non-resumable because once an exception has been raised, we cannot resume execution from where the exception was thrown. We can only handle the exception and do something else. We know that DivByZero is an exception because its effect operation has the Void return type.

Note: The Void type is an empty, i.e., uninhabited, type built into Flix. A function with the return type Void cannot return normally; it only returns abnormally (e.g., by throwing an exception). Similarly, a function that takes an argument of type Void cannot be called.

Recall that Flix supports effect polymorphism, hence the following works without issue:

def main(): Unit \ IO = 
    let l = List#{1, 2, 0, 3};
    run {
        List.map(x -> println(divide(42, x)), l);
        ()
    } with handler DivByZero {
        def divByZero(_) = println("Oops: Division by Zero!")
    }

This program will print:

42
21
Oops: Division by Zero!

Because the first two calls to divide succeed, whereas the last call will raise a DivByZero exception. Notably, the Flix type and effect system can track the exception effect through the effect polymorphic call to List.map.

Resumable Effects

Flix also supports resumable effects. For example:

import java.time.LocalDateTime

eff HourOfDay {
    def getCurrentHour(): Int32
}

def greeting(): String \ {HourOfDay} = 
    let h = HourOfDay.getCurrentHour();
    if (h <= 12) 
        "Good morning"
    else if (h <= 18)
        "Good afternoon"
    else 
        "Good evening"

def main(): Unit \ IO = 
    run {
        println(greeting())
    } with handler HourOfDay {
        def getCurrentHour(_, resume) = 
            let dt = LocalDateTime.now();
            resume(dt.getHour())
    }

Here we declare an effect HourOfDay with a single operation that returns the current hour of the day. Next, we define the greeting function, which uses the HourOfDay effect to return a greeting appropriate for the current time. Lastly, in main, we call greeting and print its result. In particular, the handler for HourOfDay uses Java interoperability to obtain the current hour.

What is important is that when the effect getHourOfDay is called, Flix captures the current continuation and finds the closest handler (in main), which resumes the computation from within greeting using the current hour of the day, as obtained from system clock.

Multiple Effects and Handlers

We can write functions that use multiple effects:

eff Ask {
    def ask(): String
}

eff Say {
    def say(s: String): Unit
}

def greeting(): Unit \ {Ask, Say} = 
    let name = Ask.ask();
    Say.say("Hello Mr. ${name}")

def main(): Unit \ IO = 
    run {
        greeting()
    } with handler Ask {
        def ask(_, resume) = resume("Bond, James Bond")
    } with handler Say {
        def say(s, resume) = { println(s); resume() }
    }

Here we declare two effects: Ask and Say. The Ask effect is a consumer: it needs a string from the environment. The Say effect is a producer: it passes a string to the environment. We use both effects in greeting. In main, we call greeting and handle each effect. We handle the Ask effect by always resuming the continuation with the string "Bond, James Bond". We handle the Say effect by printing to the console and resuming the continuation.

Multiple Resumptions

Flix supports algebraic effects with multiple resumptions. We can use such effects to implement async/await, backtracking search, cooperative multi-tasking, and more.

Here is a simple example:

eff Amb {
    def flip(): Bool
}

eff Exc {
    def raise(m: String): Void
}

def drunkFlip(): String \ {Amb, Exc} = {
    if (Amb.flip()) {
        let heads = Amb.flip();
        if (heads) "heads" else "tails"
    } else {
        Exc.raise("too drunk to flip")
    }
}

def handleAmb(f: a -> b \ ef): a -> List[b] \ ef - Amb =  
    x -> run {
        f(x) :: Nil
    } with handler Amb {
        def flip(_, resume) = resume(true) ::: resume(false)
    }

def handleExc(f: a -> b \ ef): a -> Option[b] \ ef - Exc = 
    x -> run {
        Some(f(x))
    } with handler Exc {
        def raise(_, _) = None
    }


def main(): Unit \ IO = {
    // Prints: Some(heads) :: Some(tails) :: None :: Nil
    handleAmb(handleExc(drunkFlip))() |> println;

    // Prints: None
    handleExc(handleAmb(drunkFlip))() |> println
}

Here we declare two effects: Amb (short for ambiguous) and Exc (short for exception). We then define the drunkFlip function. The idea is to model a drunk man trying to flip a coin. First, we flip a coin to determine if the man can flip the coin or if he drops it. Second, if the flip was successful, we flip the coin again to obtain either heads or tails. What is important is that drunkFlip conceptually has three outcomes: “heads”, “tails”, or “too drunk”.

Next, we define two effect handlers: handleAmb and handleExc. Starting with the latter, the Exc handler catches the exception and returns None. If no exception is raised, it returns Some(x) of the computed value. The Amb handler handles the flip effect by calling the continuation twice with true and false, and collecting the result in a list. In other words, the Amb handler explores both outcomes of flipping a coin.

In main, we use the two effect handlers. Notably, the nesting order of handlers matters! If we handle the Exc effect first then we obtain the list Some(heads) :: Some(tails) :: None :: Nil. If, on the other hand, we handle Exc last then the whole computation fails with None.

Algebraic Effects and Monads

Flix supports algebraic effect handlers and monads because we want to support both styles of programming:

• If you want to program with effect handlers, you can do that.

• If you want to program with functors, applicative functors, and monads, you can do that.

Flix does not (yet) define an IO monad, but you can roll your own.

The Flix Standard Library is biased towards a hybrid. We use algebraic effects to model interaction with the outside world but prefer the Option and Result data types for simple error handling. Working with Options and Results is more pleasant with monadic syntax.

Limitation: Polymorphic Effects

The Flix type and effect system does not yet support polymorphic effects.¹

For example, we cannot declare a polymorphic Throw[a] effect:

eff Throw[a] {
    def throw(x: a): Void
}

The Flix compiler emits the error message:

❌ -- Syntax Error --

>> Unexpected effect type parameters.

1 | eff Throw[a] {
              ^
              unexpected effect type parameters

Unfortunately, if we need to throw values of different types, we have to declare different effects.

For example:

eff ThrowBool {
    def throw(x: Bool): Void
}

eff ThrowInt32 {
    def throw(x: Int32): Void
}

Unhandled Effects in New Object and Spawn Expressions

Flix does not permit unhandled effects in new object expressions nor in spawn expressions.

For example, if we write:

eff Ask {
    def ask(): String
}

def main(): Unit \ IO = 
    region rc {
        spawn Ask.ask() @ rc
    }

The Flix compiler emits the error message:

-- Safety Error -------------------------------------------------- 

>> Illegal spawn effect: 'Ask'. 

>> A spawn expression must be pure or have a primitive effect.

7 |         spawn do Ask.ask() @ rc
                  ^^^^^^^^^^^^
                  illegal effect.

1. We are currently investigating how to lift this restriction. ↩

Default Handlers

Flix supports default handlers which means that an effect can declare a handler that translates the effect into the IO effect. This allows main (and any method annotated with @Test) to use that effect without explicitly providing a handler in a run-with block.

For example, we can write:

use Sys.Env
use Time.Clock

def main(): Unit \ {Clock, Env, Logger} =
    let ts = Clock.currentTime(TimeUnit.Milliseconds);
    let os = Env.getOsName();
    Logger.info("UNIX Timestamp:   ${ts}");
    Logger.info("Operating System: ${os}")

which the Flix compiler translates to:

use Sys.Env
use Time.Clock

def main(): Unit \ IO =
    run {
        let ts = Clock.currentTime(TimeUnit.Milliseconds);
        let os = Env.getOsName();
        Logger.info("UNIX Timestamp:   ${ts}");
        Logger.info("Operating System: ${os}")
    } with Clock.runWithIO
      with Env.runWithIO
      with Logger.runWithIO

That is, the Flix compiler automatically inserts calls to Clock.runWithIO, Env.runWithIO, and Logger.runWithIO which are the default handlers for their respective effects.

For example, Clock.runWithIO is declared as:

use Time.Clock

@DefaultHandler
pub def runWithIO(f: Unit -> a \ ef): a \ (ef - Clock) + IO = ...

A default handler is declared using the @DefaultHandler annotation. Each effect may have at most one default handler, and it must reside in the companion module of that effect.

A default handler must have a signature of the form:

def runWithIO(f: Unit -> a \ ef): a \ (ef - E) + IO

where E is the name of the effect.

We can use effects with default handlers in tests. For example:

@Test
def myTest01(): Unit \ {Assert, Logger} = 
    Logger.info("Running test!");
    Assert.assertEq(expected = 42, 42)

Effect-Oriented Programming

Programming with effects requires a new mindset, an effect-oriented mindset.

Imagine a programmer coming from JavaScript or Python to a statically-typed programming language such as C# or Java. If they continue to program with objects, maps, and strings without introducing their own types, then the benefits of a static type system are lost. In the same way, if a programmer comes to Flix without adapting an effect-oriented mindset then the benefits of the Flix type and effect system are lost.

In Flix, we can give every function the IO effect and call effectful code everywhere, but this is not effect-oriented programming and is a bad programming style. A proper effect-oriented program architecture consists of a functional core, which may use algebraic effects and handlers, surrounded by an imperative shell that performs IO. A good rule of thumb is that IO effect should be close to the main function.

We now illustrate these points with an example.

A Guessing Game — The Wrong Way

Consider the following program written in a mixed style of Flix and Java:

import java.lang.System
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.{Random => JRandom}

def getSecretNumber(): Int32 \ {NonDet, IO} = 
    let rnd = new JRandom();
    rnd.nextInt()

def readGuess(): Result[String, String] \ IO = 
    let reader = new BufferedReader(new InputStreamReader(System.in));
    let line = reader.readLine();
    if (Object.isNull(line)) 
        Result.Err("no input")
    else 
        Result.Ok(line)

def readAndParseGuess(): Result[String, Int32] \ IO = 
    forM(g <- readGuess(); 
         n <- Int32.parse(10, g)
    ) yield n

def gameLoop(secret: Int32): Unit \ IO = {
    println("Enter a guess:");
    match readAndParseGuess() {
        case Result.Ok(g) => 
            if (secret == g) {
                println("Correct!")
            } else {
                println("Incorrect!");
                gameLoop(secret)
            }
        case Result.Err(_) => 
            println("Not a number? Goodbye.");
            println("The secret was: ${secret}")
    }
}

def main(): Unit \ {NonDet, IO} = 
    let secret = getSecretNumber();
    gameLoop(secret)

Here every function, i.e. getSecretNumber, readGuess, readAndParseGuess, gameLoop, and main has the IO effect. The consequence is that every function can do anything. Note how effectful code is scattered everywhere throughout the program.

Understanding, refactoring, and testing a program written in this style is a nightmare.

Programming in a effect-oriented style means that we should define effects for every action that interacts with the outside world. We should then handle these effects close to the main function.

A Guessing Game — The Right Way

Here is what we should have done:

import java.lang.System
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.{Random => JRandom}

eff Guess {
    def readGuess(): Result[String, String]
}

eff Secret {
    def getSecret(): Int32
}

eff Terminal {
    def println(s: String): Unit    
}

def readAndParseGuess(): Result[String, Int32] \ {Guess} = 
    forM(g <- Guess.readGuess(); 
         n <- Int32.parse(10, g)
    ) yield n

def gameLoop(secret: Int32): Unit \ {Guess, Terminal} = {
    Terminal.println("Enter a guess:");
    match readAndParseGuess() {
        case Result.Ok(g) => 
            if (secret == g) {
                Terminal.println("Correct!")
            } else {
                Terminal.println("Incorrect!");
                gameLoop(secret)
            }
        case Result.Err(_) => 
            Terminal.println("Not a number? Goodbye.");
            Terminal.println("The secret was: ${secret}")
    }
}

def main(): Unit \ {NonDet, IO} = 
    run {
        let secret = Secret.getSecret();
        gameLoop(secret)
    } with handler Secret {
        def getSecret(_, resume) = 
            let rnd = new JRandom();
            resume(rnd.nextInt())
    } with handler Guess {
        def readGuess(_, resume) = 
            let reader = new BufferedReader(new InputStreamReader(System.in));
            let line = reader.readLine();
            if (Object.isNull(line)) 
                resume(Result.Err("no input"))
            else 
                resume(Result.Ok(line))
    } with handler Terminal {
        def println(s, resume) = { println(s); resume() }
    }

Here, we have introduced three algebraic effects:

1. A Guess effect that represents the action of asking the user for a guess.
2. A Secret effect that represents the action of picking a secret number.
3. A Terminal effect that represents the action of printing to the console.

We have written each function to only use the relevant effects. For example, the gameLoop function uses the Guess and Terminal effects — and has no other effects. Furthermore, all effects are now handled in one place: in the main function. The upshot is that the business is logic is purely functional. Where impurity is needed, it is precisely encapsulated by the use of effects and handlers.

Library Effects

Flix provides several built-in library effects for common I/O operations. These effects all have default handlers, so no explicit runWithIO is needed in main.

Assert

Flix provides Assert as a library effect for runtime assertions. The Assert effect has a default handler, so no explicit runWithIO call is needed in main.

Basic Assertions

The Assert module provides several assertion functions:

mod Assert {
    /// Asserts that `cond` is `true`.
    def assertTrue(cond: Bool): Unit \ Assert

    /// Asserts that `cond` is `false`.
    def assertFalse(cond: Bool): Unit \ Assert

    /// Asserts that `expected` equals `actual`.
    def assertEq(expected: a, actual: a): Unit \ Assert with Eq[a], ToString[a]

    /// Asserts that `unexpected` does not equal `actual`.
    def assertNeq(unexpected: a, actual: a): Unit \ Assert with Eq[a], ToString[a]

    /// Asserts that `o` is `Some`.
    def assertSome(o: Option[a]): Unit \ Assert

    /// Asserts that `o` is `None`.
    def assertNone(o: Option[a]): Unit \ Assert with ToString[a]

    /// Asserts that `r` is `Ok`.
    def assertOk(r: Result[e, a]): Unit \ Assert with ToString[e]

    /// Asserts that `r` is `Err`.
    def assertErr(r: Result[e, a]): Unit \ Assert with ToString[a]

    /// Asserts that `ma` is empty.
    def assertEmpty(ma: m[a]): Unit \ Assert with Foldable[m]

    /// Asserts that `ma` is non-empty.
    def assertNonEmpty(ma: m[a]): Unit \ Assert with Foldable[m]

    /// Unconditionally succeeds with the given message `msg`.
    def success(msg: String): Unit \ Assert

    /// Unconditionally fails with the given message `msg`.
    def fail(msg: String): Unit \ Assert
}

Using Assert with the Default Handler

The default handler throws an AssertionError on failure, so no explicit handler is needed:

use Assert.{assertTrue, assertFalse, assertEq, assertNeq}

def main(): Unit \ { Assert, IO } =
    assertTrue(1 + 1 == 2);
    assertFalse(1 > 2);
    assertEq(expected = 4, 2 + 2);
    assertNeq(unexpected = 0, 1 + 1);
    println("All assertions passed!")

Printing Failures to Standard Out

The runWithStdOut handler prints assertion failures to standard out but allows execution to continue:

use Assert.assertEq

def main(): Unit \ IO =
    run {
        assertEq(expected = 4, 2 + 2);
        assertEq(expected = 10, 3 + 3);
        println("Execution continued after failing assertion.")
    } with Assert.runWithStdOut

Logging Failures with the Logger

The runWithLogger handler sends assertion failures to the Logger effect:

use Assert.assertEq

def main(): Unit \ IO =
    run {
        assertEq(expected = 42, 21 + 21);
        assertEq(expected = 10, 3 + 3);
        println("Execution continued after failing assertion.")
    } with Assert.runWithLogger
      with Logger.runWithIO

Clock

Flix provides Clock as a library effect for querying the current wall-clock time. The Clock effect has a default handler, so no explicit runWithIO call is needed in main. The key module is Time.Clock.

The Clock Effect

The Clock effect has a single operation that returns the time since the epoch in a given unit:

pub eff Clock {
    /// Returns a measure of time since the epoch in the given time unit `u`.
    def currentTime(u: TimeUnit): Int64
}

The TimeUnit enum determines the granularity of the result:

pub enum TimeUnit with Eq, ToString {
    case Days,
    case Hours,
    case Microseconds,
    case Milliseconds,
    case Minutes,
    case Nanoseconds,
    case Seconds
}

Reading the Current Time

The simplest use of Clock is to read the current time and print it:

use Time.Clock
use Time.TimeUnit

def main(): Unit \ { Clock, IO } =
    let timestamp = Clock.currentTime(TimeUnit.Milliseconds);
    println("${timestamp} ms since the epoch")

Because Clock has a default handler, the effect is handled automatically.

The now Function

The Clock.now function is a shorthand for Clock.currentTime(TimeUnit.Milliseconds):

use Time.Clock

def main(): Unit \ { Clock, IO } =
    let before = Clock.now();
    // ... do some work ...
    let after = Clock.now();
    println("Elapsed: ${after - before} ms")

Console

Flix provides Console as a library effect for terminal I/O. The Console effect has a default handler, so no explicit runWithIO call is needed in main. The key module is Sys.Console.

The Console Effect

The Console effect supports reading from standard input and writing to standard output and standard error:

pub eff Console {
    /// Reads a single line from the console.
    def readln(): String

    /// Prints the given string `s` to the standard out.
    def print(s: String): Unit

    /// Prints the given string `s` to the standard err.
    def eprint(s: String): Unit

    /// Prints the given string `s` to the standard out followed by a new line.
    def println(s: String): Unit

    /// Prints the given string `s` to the standard err followed by a new line.
    def eprintln(s: String): Unit
}

The Console Module

The Console module provides several higher-level functions built on the Console effect:

mod Sys.Console {
    /// Prints prompt `p`, reads a line, and returns `default` if the input is empty.
    def readlnWithDefault(p: a, default: String): String \ Console

    /// Prints prompt `p`, reads a line, and applies `f` to the input.
    /// Re-prompts on `Err(msg)`, returns `v` on `Ok(v)`.
    def readlnWith(p: a, f: String -> Result[String, b]): b \ Console

    /// Prints prompt `p` with a yes/no hint and reads a boolean answer.
    /// Empty or unrecognized input returns `default`.
    def confirm(p: a, default: {default = Bool}): Bool \ Console

    /// Prints prompt `p` with a numbered list of choices and reads a selection.
    /// Returns `None` if the input is invalid.
    def pick(p: a, choices: List[b]): Option[b] \ Console

    /// Like `pick`, but re-prompts until the user makes a valid selection.
    def pickWith(p: a, choices: List[b]): b \ Console
}

Basic Console I/O

The simplest use of Console is to print a prompt, read input, and respond:

use Sys.Console

def main(): Unit \ Console =
    Console.print("What is your name? ");
    let name = Console.readln();
    Console.println("Hello ${name}!")

Confirmed Input

The Console.confirm function asks a yes/no question and returns a Bool. You can supply a default value that is used when the user presses Enter without typing anything:

use Sys.Console

def main(): Unit \ Console =
    let proceed = Console.confirm("Deploy to production?", default = true);
    if (proceed)
        Console.println("Deploying...")
    else
        Console.println("Aborted.")

Validated Input

The Console.readlnWith function repeatedly prompts the user until the input passes a validator. The validator returns Ok(value) on success or Err(message) to re-prompt:

use Sys.Console

def main(): Unit \ Console =
    let n = Console.readlnWith("Enter a number (1-10): ", s ->
        match Int32.fromString(s) {
            case Some(i) if i >= 1 and i <= 10 => Ok(i)
            case _ => Err("Please enter a number between 1 and 10.")
        }
    );
    Console.println("You entered: ${n}")

Env

Flix provides Env as a library effect for accessing environment variables, system properties, and platform information. The Env effect has a default handler, so no explicit runWithIO call is needed in main. The key module is Sys.Env.

The Env Effect

The Env effect provides operations for reading the program’s environment:

pub eff Env {
    /// Returns the arguments passed to the program via the command line.
    def getArgs(): List[String]

    /// Returns a map of the current system environment.
    def getEnv(): Map[String, String]

    /// Returns the value of the specified environment variable.
    def getVar(name: String): Option[String]

    /// Returns the system property by name.
    def getProp(name: String): Option[String]

    /// Returns the operating system name.
    def getOsName(): Option[String]

    /// Returns the operating system architecture.
    def getOsArch(): Option[String]

    /// Returns the operating system version.
    def getOsVersion(): Option[String]

    /// Returns the file separator.
    def getFileSeparator(): String

    /// Returns the path separator.
    def getPathSeparator(): String

    /// Returns the system line separator.
    def getLineSeparator(): String

    /// Returns the user's current working directory.
    def getCurrentWorkingDirectory(): Option[String]

    /// Returns the default temp file path.
    def getTemporaryDirectory(): Option[String]

    /// Returns the user's account name.
    def getUserName(): Option[String]

    /// Returns the user's home directory.
    def getUserHomeDirectory(): Option[String]

    /// Returns the number of virtual processors available to the JVM.
    def getVirtualProcessors(): Int32
}

Directories and OS Info

The simplest use of Env is to query the current directory, home directory, or operating system:

use Sys.Env

def main(): Unit \ { Env, IO } =
    let home = Env.getUserHomeDirectory();
    println("Home: ${home}");
    let cwd = Env.getCurrentWorkingDirectory();
    println("CWD: ${cwd}");
    let os = Env.getOsName();
    println("OS: ${os}")

Environment Variables

Use getVar to read a single environment variable, or getEnv to retrieve all of them as a map:

use Sys.Env

def main(): Unit \ { Env, IO } =
    let path = Env.getVar("PATH");
    println("PATH: ${path}");
    let all = Env.getEnv();
    println("Total env vars: ${Map.size(all)}")

System Information

The Env effect also exposes platform details such as the OS architecture and the number of available processors:

use Sys.Env

def main(): Unit \ { Env, IO } =
    let name    = Env.getOsName();
    let arch    = Env.getOsArch();
    let version = Env.getOsVersion();
    let cpus    = Env.getVirtualProcessors();
    println("OS:   ${name}");
    println("Arch: ${arch}");
    println("Ver:  ${version}");
    println("CPUs: ${cpus}")

Exit

Flix provides Exit as a library effect for terminating the program. The Exit effect has a default handler, so no explicit runWithIO call is needed in main. The key module is Sys.Exit.

The Exit Effect

The Exit effect has a single operation that immediately stops the JVM with a given exit code:

pub eff Exit {
    /// Immediately exits the JVM with the specified `exitCode`.
    def exit(exitCode: Int32): Void
}

The return type Void indicates that exit never returns normally.

Exiting the Program

The simplest use of Exit is to terminate with a specific exit code:

use Sys.Exit

def main(): Unit \ { Exit, IO } =
    println("Goodbye!");
    Exit.exit(0)

A zero exit code conventionally signals success, while a non-zero code signals an error.

FileSystem

Flix provides a family of effects for filesystem operations. The key modules are:

• Fs.FileSystem — the unified FileSystem effect (all 29 operations)
• Fs.FileRead — the FileRead effect (read, readLines, readBytes)
• Fs.FileWrite — the FileWrite effect (write, append, delete, copy, move, mkdir, etc.)
• Fs.FileStat — the FileStat effect (exists, type tests, permissions, timestamps, size)
• Fs.DirList — the DirList effect (listing directory contents)
• Fs.Glob — the Glob effect (finding files by pattern)
• Fs.Size — utilities for working with file sizes

All effects have default handlers, so no explicit runWithIO call is needed in main.

There are also more fine-grained leaf effects (e.g. FileExists, ReadFile, WriteFile) that do not have default handlers but can be run into their parent effects using runWith handlers. See The Effect Hierarchy for details.

Reading a File

We can use FileRead.read to read an entire file as a string:

use Fs.FileRead

def main(): Unit \ { FileRead, IO } =
    match FileRead.read("example.txt") {
        case Ok(content) => println(content)
        case Err(err)    => println("Error: ${err}")
    }

All filesystem operations return Result[IoError, ...]. The IoError type is a pair of an ErrorKind and a message string. The ErrorKind enum tells us what went wrong:

Note: The IO effect appears in the signature because of println.

Writing a File

We can use FileWrite.write to write a string to a file:

use Fs.FileWrite

def main(): Unit \ { FileWrite, IO } =
    match FileWrite.write(str = "Hello, Flix!", "greeting.txt") {
        case Ok(_)    => println("File written successfully.")
        case Err(err) => println("Error: ${err}")
    }

Reading and Writing Lines

We can use readLines and writeLines to work with files line by line:

use Fs.FileRead
use Fs.FileWrite

def main(): Unit \ { FileRead, FileWrite, IO } =
    match FileWrite.writeLines(lines = List#{"Line 1", "Line 2", "Line 3"}, "data.txt") {
        case Err(err) => println("Write error: ${err}")
        case Ok(_) =>
            match FileRead.readLines("data.txt") {
                case Ok(lines) =>
                    foreach (line <- lines) {
                        println(line)
                    }
                case Err(err) => println("Read error: ${err}")
            }
    }

Note: Since we both read and write, the effect set includes FileRead, FileWrite, and IO.

Reading and Writing Bytes

We can use readBytes and writeBytes for binary data:

use Fs.FileRead
use Fs.FileWrite

def main(): Unit \ { FileRead, FileWrite, IO } =
    let data = Vector#{72i8, 101i8, 108i8, 108i8, 111i8};
    match FileWrite.writeBytes(data, "binary.dat") {
        case Err(err) => println("Write error: ${err}")
        case Ok(_) =>
            match FileRead.readBytes("binary.dat") {
                case Ok(bytes) =>
                    println("Read ${Vector.length(bytes)} bytes.");
                    println("As string: ${String.fromBytes(bytes)}")
                case Err(err) => println("Read error: ${err}")
            }
    }

Appending to a File

We can use append to add text to an existing file without overwriting it. The file is created if it does not exist:

use Fs.FileRead
use Fs.FileWrite

def main(): Unit \ { FileRead, FileWrite, IO } =
    match FileWrite.write(str = "Line 1\n", "log.txt") {
        case Err(err) => println("Write error: ${err}")
        case Ok(_) =>
            match FileWrite.append(str = "Line 2\n", "log.txt") {
                case Err(err) => println("Append error: ${err}")
                case Ok(_) =>
                    match FileRead.read("log.txt") {
                        case Ok(content) => println(content)
                        case Err(err)    => println("Read error: ${err}")
                    }
            }
    }

There are also appendLines and appendBytes variants.

Listing a Directory

We can use DirList.list to get the names of all files and directories in a directory:

use Fs.DirList

def main(): Unit \ { DirList, IO } =
    match DirList.list(".") {
        case Ok(entries) =>
            foreach (entry <- entries) {
                println(entry)
            }
        case Err(err) => println("Error: ${err}")
    }

Finding Files with Glob

We can use Glob.glob to find files matching a glob pattern under a base directory:

use Fs.Glob

def main(): Unit \ { Glob, IO } =
    match Glob.glob(".", "*.flix") {
        case Ok(files) =>
            foreach (file <- files) {
                println(file)
            }
        case Err(err) => println("Error: ${err}")
    }

File Metadata

We can use the FileStat effect to inspect file metadata: existence, type, size, permissions, and timestamps:

use Fs.FileStat
use Fs.FileWrite

def main(): Unit \ { FileStat, FileWrite, IO } =
    let file = "example.txt";
    match FileWrite.write(str = "Hello!", file) {
        case Err(err) => println("Write error: ${err}")
        case Ok(_) =>
            match FileStat.exists(file) {
                case Ok(b)    => println("Exists: ${b}")
                case Err(err) => println("Error: ${err}")
            };
            match FileStat.isRegularFile(file) {
                case Ok(b)    => println("Is regular file: ${b}")
                case Err(err) => println("Error: ${err}")
            };
            match FileStat.isDirectory(file) {
                case Ok(b)    => println("Is directory: ${b}")
                case Err(err) => println("Error: ${err}")
            };
            match FileStat.size(file) {
                case Ok(s)    => println("Size: ${s}")
                case Err(err) => println("Error: ${err}")
            };
            match FileStat.modificationTime(file) {
                case Ok(t)    => println("Modification time: ${t}ms")
                case Err(err) => println("Error: ${err}")
            }
    }

The FileStat effect combines four sub-effects:

Copying, Moving, and Deleting

We can also use the FileWrite effect to copy, move, and delete files:

use Fs.FileWrite

def main(): Unit \ { FileWrite, IO } =
    match FileWrite.write(str = "Hello!", "original.txt") {
        case Err(err) => println("Write error: ${err}")
        case Ok(_) =>
            // Copy with no options.
            match FileWrite.copy(src = "original.txt", "copy.txt") {
                case Ok(_)    => println("Copied.")
                case Err(err) => println("Copy error: ${err}")
            };
            // Move (rename) with no options.
            match FileWrite.move(src = "copy.txt", "renamed.txt") {
                case Ok(_)    => println("Moved.")
                case Err(err) => println("Move error: ${err}")
            };
            // Delete.
            match FileWrite.delete("renamed.txt") {
                case Ok(_)    => println("Deleted.")
                case Err(err) => println("Delete error: ${err}")
            }
    }

The copy and move functions are convenience wrappers around copyWith and moveWith, which accept option sets:

• CopyOption.CopyAttributes — preserve file attributes
• CopyOption.ReplaceExisting — overwrite the destination if it exists
• MoveOption.AtomicMove — perform an atomic rename
• MoveOption.ReplaceExisting — overwrite the destination if it exists

Creating Directories

We can use mkDir to create a single directory, mkDirs to create a directory and all its parents, and mkTempDir to create a temporary directory:

use Fs.FileWrite

def main(): Unit \ { FileWrite, IO } =
    match FileWrite.mkDirs("a/b/c") {
        case Ok(_)    => println("Created a/b/c.")
        case Err(err) => println("Error: ${err}")
    };
    match FileWrite.mkTempDir("flix-") {
        case Ok(path) => println("Temp dir: ${path}")
        case Err(err) => println("Error: ${err}")
    }

The FileSystem Effect

The FileSystem effect combines all filesystem operations into a single effect. It includes all operations from FileStat, FileRead, FileWrite, DirList, and Glob. We can use FileSystem when we need multiple categories of operations together:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    match FileSystem.write(str = "Hello!", "greeting.txt") {
        case Err(err) => println("Write error: ${err}")
        case Ok(_) =>
            match FileSystem.read("greeting.txt") {
                case Ok(content) => println("Read: ${content}")
                case Err(err)    => println("Read error: ${err}")
            }
    }

Middleware

Middleware are effect handlers that intercept filesystem operations. We apply them using run { ... } with FileSystem.<middleware> (or the corresponding sub-effect module) and compose them by stacking multiple with clauses.

Base Directory

withBaseDir resolves relative paths against a base directory. Absolute paths pass through unchanged:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    match FileSystem.mkDirs("/tmp/flix-basedir") {
        case Err(err) => println("Setup error: ${err}")
        case Ok(_) =>
            run {
                match FileSystem.write(str = "Hello", "greeting.txt") {
                    case Err(err) => println("Write error: ${err}")
                    case Ok(_) =>
                        match FileSystem.read("greeting.txt") {
                            case Ok(content) => println("Read: ${content}")
                            case Err(err)    => println("Read error: ${err}")
                        }
                }
            } with FileSystem.withBaseDir("/tmp/flix-basedir")
    }

Chroot

withChroot restricts all operations to a directory subtree. Operations targeting paths outside the chroot fail with a PermissionDenied error:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    match FileSystem.mkDirs("/tmp/flix-chroot") {
        case Err(err) => println("Setup error: ${err}")
        case Ok(_) =>
            run {
                match FileSystem.write(str = "Hello", "/tmp/flix-chroot/data.txt") {
                    case Ok(_)    => println("Write inside chroot succeeded")
                    case Err(err) => println("Error: ${err}")
                };
                match FileSystem.read("/etc/hostname") {
                    case Ok(_)    => println("Unexpected: read outside chroot succeeded")
                    case Err(err) => println("Read outside chroot blocked: ${err}")
                }
            } with FileSystem.withChroot("/tmp/flix-chroot")
    }

Logging

withLogging logs each filesystem operation via the Logger effect. Note that Logger appears in the type signature of main:

use Fs.FileSystem

def main(): Unit \ { FileSystem, Logger, IO } =
    run {
        match FileSystem.write(str = "Hello, Flix!", "greeting.txt") {
            case Err(err) => println("Write error: ${err}")
            case Ok(_) =>
                match FileSystem.read("greeting.txt") {
                    case Ok(content) => println(content)
                    case Err(err)    => println("Read error: ${err}")
                }
        }
    } with FileSystem.withLogging

Read-Only

withReadOnly blocks all write operations with a PermissionDenied error. Read and stat operations pass through normally:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    run {
        match FileSystem.write(str = "This will fail", "blocked.txt") {
            case Ok(_)    => println("Unexpected: write succeeded")
            case Err(err) => println("Write blocked: ${err}")
        };
        match FileSystem.exists("blocked.txt") {
            case Ok(b)    => println("Exists: ${b}")
            case Err(err) => println("Error: ${err}")
        }
    } with FileSystem.withReadOnly

Dry Run

withDryRun logs write operations via the Logger effect without performing them. Read operations still execute normally:

use Fs.FileSystem

def main(): Unit \ { FileSystem, Logger, IO } =
    run {
        match FileSystem.write(str = "This won't be written", "phantom.txt") {
            case Err(err) => println("Write error: ${err}")
            case Ok(_) =>
                match FileSystem.exists("phantom.txt") {
                    case Ok(b)    => println("Exists: ${b}")
                    case Err(err) => println("Error: ${err}")
                }
        }
    } with FileSystem.withDryRun

Atomic Write

withAtomicWrite writes data to a temporary file first, then atomically renames it into place. This prevents partial writes on failure. Only write, writeLines, and writeBytes are affected — appends and other operations pass through unchanged:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    run {
        match FileSystem.write(str = "Atomic content", "output.txt") {
            case Ok(_)    => println("Atomic write succeeded.")
            case Err(err) => println("Write error: ${err}")
        }
    } with FileSystem.withAtomicWrite

Backup

withBackup creates a backup copy of existing files before overwriting them. Before each destructive operation (write, writeLines, writeBytes, truncate, delete, copyWith, moveWith), the existing file is copied to file + suffix:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    match FileSystem.write(str = "Original content", "data.txt") {
        case Err(err) => println("Setup error: ${err}")
        case Ok(_) =>
            run {
                match FileSystem.write(str = "New content", "data.txt") {
                    case Ok(_)    => println("Write succeeded; backup saved to data.txt.bak")
                    case Err(err) => println("Write error: ${err}")
                }
            } with FileSystem.withBackup(".bak")
    }

Create Parent Directories

withMkParentDirs automatically creates parent directories before write and append operations. If the parent directory already exists, this is a no-op:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    run {
        match FileSystem.write(str = "Hello", "deep/nested/path/greeting.txt") {
            case Ok(_)    => println("Write succeeded (parents created).")
            case Err(err) => println("Write error: ${err}")
        }
    } with FileSystem.withMkParentDirs

Conflict Check

withConflictCheck tracks file modification times and rejects writes when the file has been modified externally since the last operation. This catches write-write conflicts from external processes:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    run {
        match FileSystem.write(str = "First write", "shared.txt") {
            case Err(err) => println("Error: ${err}")
            case Ok(_) =>
                match FileSystem.write(str = "Second write", "shared.txt") {
                    case Ok(_)    => println("No conflict detected.")
                    case Err(err) => println("Conflict: ${err}")
                }
        }
    } with FileSystem.withConflictCheck

Transfer Limit

withTransferLimit rejects read or write operations where the payload exceeds a maximum size:

use Fs.FileSystem
use Fs.Size

def main(): Unit \ { FileSystem, IO } =
    run {
        match FileSystem.write(str = "Small", "ok.txt") {
            case Ok(_)    => println("Small write succeeded.")
            case Err(err) => println("Error: ${err}")
        }
    } with FileSystem.withTransferLimit(Size.megaBytes(10))

Access Control

Flix provides middleware for restricting which paths can be accessed. We can use:

• withAllowList(dirs) — only paths within the listed directories are allowed
• withDenyList(dirs) — paths within the listed directories are blocked
• withAllowGlob(patterns) — only paths matching at least one pattern are allowed
• withDenyGlob(patterns) — paths matching any pattern are blocked

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    run {
        match FileSystem.read("/tmp/safe/data.txt") {
            case Ok(content) => println(content)
            case Err(err)    => println("Error: ${err}")
        }
    } with FileSystem.withAllowList(Nel.of("/tmp/safe"))

In-Memory Filesystem

The withInMemoryFS handler replaces the real filesystem with a fully in-memory implementation. The filesystem starts empty; reads of non-written files return NotFound. No real filesystem access occurs:

use Fs.FileSystem
use Time.Clock

def main(): Unit \ { Clock, IO } =
    run {
        let result = forM (
            _       <- FileSystem.mkDirs("/data");
            _       <- FileSystem.write(str = "Hello", "/data/hello.txt");
            _       <- FileSystem.write(str = "World", "/data/world.txt");
            entries <- FileSystem.list("/data");
            content <- FileSystem.read("/data/hello.txt");
            _       <- FileSystem.delete("/data/hello.txt");
            exists  <- FileSystem.exists("/data/hello.txt")
        ) yield (entries, content, exists);
        match result {
            case Err(err) => println("Error: ${err}")
            case Ok((entries, content, exists)) =>
                println("Files in /data:");
                foreach (entry <- entries) {
                    println("  ${entry}")
                };
                println("Content: ${content}");
                println("Exists after delete: ${exists}")
        }
    } with FileSystem.withInMemoryFS

Note that withInMemoryFS requires the Clock effect (for file timestamps) but removes FileSystem from the effect signature since it fully handles it.

Memory Overlay

The withMemoryOverlay handler layers an in-memory writable store on top of the real filesystem. Writes are captured in memory and subsequent reads see the written data, but the real filesystem is never modified. Reads of files not in the overlay fall through to the real filesystem:

use Fs.FileSystem

def main(): Unit \ { FileSystem, IO } =
    run {
        // This write is captured in memory, not written to disk.
        match FileSystem.write(str = "In-memory only", "virtual.txt") {
            case Err(err) => println("Error: ${err}")
            case Ok(_) =>
                match FileSystem.read("virtual.txt") {
                    case Ok(content) => println("Read from overlay: ${content}")
                    case Err(err)    => println("Error: ${err}")
                }
        }
    } with FileSystem.withMemoryOverlay

Composing Middleware

We can compose middleware by stacking with clauses. The innermost handler (listed first) intercepts the original operation, and then delegates to the next outer handler. Here is an example that stacks base directory, parent directory creation, backup, atomic writes, conflict checking, and logging:

use Fs.FileSystem

def main(): Unit \ { FileSystem, Logger, IO } =
    run {
        match FileSystem.write(str = "Hello, Flix!", "data/greeting.txt") {
            case Err(err) => println("Write error: ${err}")
            case Ok(_) =>
                match FileSystem.read("data/greeting.txt") {
                    case Ok(content) => println("Read: ${content}")
                    case Err(err)    => println("Read error: ${err}")
                }
        }
    } with FileSystem.withBaseDir("/tmp/flix-example")
      with FileSystem.withMkParentDirs
      with FileSystem.withConflictCheck
      with FileSystem.withBackup(".bak")
      with FileSystem.withAtomicWrite
      with FileSystem.withLogging

The FileSystem and Logger effects both have default handlers, so they are handled automatically when they appear in the type signature of main.

Note: The order of with clauses matters. The outermost handler (listed last) wraps all inner handlers. In the example above, withLogging is outermost, so it sees every filesystem operation — including retries from conflict checks and temporary files from atomic writes. When composing middleware, think about which layer should observe which operations.

Middleware Summary

The following table shows which middleware are available on which effects (scroll right to see the full table):

The Effect Hierarchy

The Flix filesystem effects form a hierarchy. At the top is FileSystem with all 29 operations. Below it are intermediate effects that group related operations, and at the bottom are leaf effects for individual operations:

FileSystem                          (29 ops — unified root)
├── FileStat                        (11 ops)
│   ├── FileTest                    (4 ops: exists, isDirectory, isRegularFile, isSymbolicLink)
│   ├── FilePermission              (3 ops: isReadable, isWritable, isExecutable)
│   ├── FileTime                    (3 ops: accessTime, creationTime, modificationTime)
│   └── FileSize                    (1 op: size)
├── FileRead                        (3 ops: read, readLines, readBytes)
├── DirList                         (1 op: list)
├── Glob                            (1 op: glob)
└── FileWrite                       (13 ops: write, append, delete, copy, move, mkdir, etc.)

We can use any level of the hierarchy. For example, we can use a leaf effect like FileExists when we only need exists, FileRead when we need to read files, or FileSystem when we need everything.

We can run leaf effects into their parent effects using runWith handlers. For example, we can run FileExists into FileTest and ReadFile into FileRead:

use Fs.FileExists
use Fs.FileRead
use Fs.FileTest
use Fs.ReadFile

def main(): Unit \ { FileRead, FileTest, IO } =
    run {
        safeRead("example.txt")
    } with FileExists.runWithFileTest
      with ReadFile.runWithFileRead

def safeRead(file: String): Unit \ { FileExists, ReadFile, IO } =
    match FileExists.exists(file) {
        case Err(err)  => println("Error: ${err}")
        case Ok(false) => println("File does not exist")
        case Ok(true)  =>
            match ReadFile.read(file) {
                case Ok(content) => println(content)
                case Err(err)    => println("Read error: ${err}")
            }
    }

Http and Https

Flix provides Http and Https as library effects for sending HTTP requests. Both effects have default handlers, so no explicit runWithIO call is needed in main. The key modules are:

• Net.Http — the Http effect and convenience functions (get, post, send, etc.)
• Net.Https — the Https effect (enforces https:// URLs)
• Net.HttpRequest — a fluent API for building requests
• Net.HttpResponse — accessors for inspecting responses
• Net.Retry — retry strategies for use with middleware

Sending a GET Request

The simplest way to make an HTTP request is with Http.get. It returns a Result[IoError, HttpResponse], so we pattern match on Ok and Err:

use Net.Http
use Net.HttpResponse

def main(): Unit \ { Http, IO } =
    match Http.get("http://example.com/") {
        case Ok(resp) => println(HttpResponse.body(resp))
        case Err(err) => println(err)
    }

The Http effect supports both http:// and https:// URLs. The effect appears in the type signature of main alongside IO.

Inspecting the Response

The HttpResponse module provides accessors for status codes, headers, and body content. The expect function returns Err for non-2xx status codes, which is useful when you want to treat unsuccessful responses as errors:

use Net.Http
use Net.HttpResponse

def main(): Unit \ { Http, IO } =
    match Http.get("https://flix.dev/") {
        case Ok(resp) =>
            println("Status:         ${HttpResponse.status(resp)}");
            println("Is success?     ${HttpResponse.isSuccess(resp)}");
            println("Is client err?  ${HttpResponse.isClientError(resp)}");
            println("Is server err?  ${HttpResponse.isServerError(resp)}");
            println("Content-Type:   ${HttpResponse.contentType(resp)}");
            println("Content-Length: ${HttpResponse.contentLength(resp)}");
            println("Server header:  ${HttpResponse.headerValue("server", resp)}");
            match HttpResponse.expect(resp) {
                case Ok(r) =>
                    println("Body length: ${String.length(HttpResponse.body(r))}")
                case Err(e) =>
                    println("Unexpected status: ${e}")
            }
        case Err(err) =>
            println("Error: ${err}")
    }

POST Requests and JSON

Use HttpRequest.post to create a POST request with a body. The request builder supports withContentType and withAccept for setting common headers. Send the built request with Http.send:

use Net.Http
use Net.HttpRequest
use Net.HttpResponse

def main(): Unit \ { Http, IO } =
    let body = "{\"name\": \"Asterix\", \"age\": 35}";
    let req = HttpRequest.post("https://flix.dev/api/users", body)
                |> HttpRequest.withContentType("application/json")
                |> HttpRequest.withAccept("application/json");
    match Http.send(req) {
        case Ok(resp) =>
            println("Status: ${HttpResponse.status(resp)}");
            println("Body: ${HttpResponse.body(resp)}")
        case Err(err) =>
            println("Error: ${err}")
    }

Building Requests

The HttpRequest module provides a fluent API for building requests. You can add query parameters, authentication tokens, custom headers, and timeouts using a pipeline of |> calls:

use Net.Http
use Net.HttpRequest
use Net.HttpResponse
use Time.Duration.seconds

def main(): Unit \ { Http, IO } =
    let req =
        HttpRequest.get("https://flix.dev/api/search")
            |> HttpRequest.withQueryParam("q", "flix programming language")
            |> HttpRequest.withQueryParams(Map#{
                "page" => "1", "per_page" => "25", "sort" => "relevance"
            })
            |> HttpRequest.withBearerToken("ghp_aBcDeFgHiJkLmNoPqRsTuVwXyZ")
            |> HttpRequest.withHeader("User-Agent", "MyApp/1.0")
            |> HttpRequest.withTimeout(seconds(5));
    match Http.send(req) {
        case Ok(resp) =>
            println("Status: ${HttpResponse.status(resp)}");
            println("Body: ${String.takeLeft(80, HttpResponse.body(resp))}")
        case Err(err) =>
            println("Error: ${err}")
    }

Constructors are available for all HTTP methods: HttpRequest.get, HttpRequest.post, HttpRequest.put, HttpRequest.patch, and HttpRequest.delete.

The Https Effect

The Https effect works like Http but enforces that all URLs use the https:// scheme. If you pass an http:// URL, the request is rejected. Use Https when you want the type system to guarantee that only secure connections are made:

use Net.Https
use Net.HttpResponse

def main(): Unit \ { Https, IO } =
    match Https.get("https://example.com/") {
        case Ok(resp) => println(HttpResponse.body(resp))
        case Err(err) => println(err)
    }

Note that Http already supports https:// URLs — Https is for when you want the effect signature to make the security guarantee explicit.

Middleware

Middleware are effect handlers that intercept Http (or Https) requests. They are applied using run { ... } with Http.<middleware> and compose by stacking multiple with clauses.

Base URL

withBaseUrl prefixes relative paths with a base URL. Absolute URLs (containing ://) bypass the base and are sent as-is:

use Net.Http
use Net.HttpResponse

def main(): Unit \ { Http, IO } =
    run {
        match Http.get("/api/users") {
            case Ok(resp) => println("/api/users -> ${HttpResponse.status(resp)}")
            case Err(err) => println("/api/users -> ${err}")
        };
        match Http.get("/api/posts") {
            case Ok(resp) => println("/api/posts -> ${HttpResponse.status(resp)}")
            case Err(err) => println("/api/posts -> ${err}")
        };
        // Absolute URLs bypass the base.
        match Http.get("https://flix.dev/other") {
            case Ok(resp) => println("absolute   -> ${HttpResponse.status(resp)}")
            case Err(err) => println("absolute   -> ${err}")
        }
    } with Http.withBaseUrl("https://flix.dev")

Default Headers

withDefaultHeaders injects headers into every request. Headers already present on a request are not overridden:

use Net.Http
use Net.HttpResponse

def main(): Unit \ { Http, IO } =
    let defaults = Map#{
        "Accept"        => List#{"application/json"},
        "Authorization" => List#{"Bearer ghp_aBcDeFgHiJkLmNoPqRsTuVwXyZ0123456789"}
    };
    run {
        match Http.get("https://flix.dev/api/users") {
            case Ok(resp) => println("Status: ${HttpResponse.status(resp)}")
            case Err(err) => println("Error: ${err}")
        }
    } with Http.withDefaultHeaders(defaults)

Logging

withLogging logs each request and response via the Logger effect. Note that Logger appears in the type signature of main:

use Net.Http
use Net.HttpResponse

def main(): Unit \ { Http, Logger, IO } =
    run {
        match Http.get("https://flix.dev/") {
            case Ok(resp) => println("Status: ${HttpResponse.status(resp)}")
            case Err(err) => println("Error: ${err}")
        };
        match Http.get("https://notfound.flix.dev/") {
            case Ok(resp) => println("Status: ${HttpResponse.status(resp)}")
            case Err(err) => println("Error: ${err}")
        }
    } with Http.withLogging

Retries

withRetry adds automatic retries using strategies from the Net.Retry module. Each strategy is a function that decides whether to retry based on the attempt number and the outcome (transport error or HTTP error):

use Net.Http
use Net.Retry
use Net.HttpResponse
use Time.Duration.milliseconds

def main(): Unit \ { Http, IO } =
    // Linear: retry up to 3 times with 100ms delay.
    run {
        println("--- Linear retry ---");
        match Http.get("https://notfound.flix.dev/") {
            case Ok(resp) => println("Status: ${HttpResponse.status(resp)}")
            case Err(err) => println("Error: ${err}")
        }
    } with Http.withRetry(Retry.linear(maxRetries = 3, delay = milliseconds(100)));

    // Exponential: retry up to 3 times with 100ms base delay.
    run {
        println("--- Exponential retry ---");
        match Http.get("https://notfound.flix.dev/") {
            case Ok(resp) => println("Status: ${HttpResponse.status(resp)}")
            case Err(err) => println("Error: ${err}")
        }
    } with Http.withRetry(Retry.exponential(maxRetries = 3, baseDelay = milliseconds(100)));

    // Transport-only: only retry on connection failures, not HTTP errors.
    run {
        println("--- Transport-only retry ---");
        match Http.get("https://notfound.flix.dev/") {
            case Ok(resp) => println("Status: ${HttpResponse.status(resp)}")
            case Err(err) => println("Error: ${err}")
        }
    } with Http.withRetry(Retry.retryTransportOnly(maxRetries = 2, delay = milliseconds(100)))

The available strategies are:

• Retry.linear — fixed delay between retries
• Retry.exponential — doubling delay between retries
• Retry.retryAfter — honours the Retry-After response header on 429/503 responses
• Retry.retryTransportOnly — retries only on connection failures, not HTTP errors

Strategies can be wrapped with Retry.withJitter to add random jitter to delays, and Retry.withDeadline to enforce a total time budget across all retries.

Circuit Breaker

withCircuitBreaker protects against cascading failures. After failureThreshold consecutive failures (transport errors or 5xx responses), the circuit opens and immediately rejects requests for the cooldown duration. A successful request resets the failure counter. Note that the Clock effect appears in the type signature:

use Net.Http
use Net.HttpResponse
use Time.Clock
use Time.Duration.seconds

def main(): Unit \ { Clock, Http, IO } =
    run {
        let urls = List#{"/a", "/b", "/c", "/d", "/e", "/f", "/g", "/h"};
        foreach (url <- urls) {
            match Http.get(url) {
                case Ok(resp) => println("${url} -> ${HttpResponse.status(resp)}")
                case Err(err) => println("${url} -> ${err}")
            }
        }
    } with Http.withCircuitBreaker(failureThreshold = 3, cooldown = seconds(5))
      with Http.withBaseUrl("https://notfound.flix.dev")

Rate Limiting

Flix provides three rate-limiting strategies:

• withMinInterval — enforces a fixed minimum delay between consecutive requests
• withTokenBucket — allows a burst of requests up front, then a steady rate
• withSlidingWindow — allows at most N requests in any rolling time window

All three require the Clock effect:

use Net.Http
use Net.HttpResponse
use Time.Clock
use Time.Duration.{milliseconds, seconds}

def main(): Unit \ { Clock, Http, IO } =
    // Min interval: at least 100ms between consecutive requests.
    run {
        println("--- Min interval ---");
        let urls = List#{"/a", "/b", "/c", "/d"};
        foreach (url <- urls) {
            match Http.get(url) {
                case Ok(resp) => println("${url} -> ${HttpResponse.status(resp)}")
                case Err(err) => println("${url} -> ${err}")
            }
        }
    } with Http.withMinInterval(interval = milliseconds(100))
      with Http.withBaseUrl("https://flix.dev");

    // Token bucket: burst of 2, then 1 request per 100ms.
    run {
        println("--- Token bucket ---");
        let urls = List#{"/a", "/b", "/c", "/d"};
        foreach (url <- urls) {
            match Http.get(url) {
                case Ok(resp) => println("${url} -> ${HttpResponse.status(resp)}")
                case Err(err) => println("${url} -> ${err}")
            }
        }
    } with Http.withTokenBucket(burstSize = 2, interval = milliseconds(100))
      with Http.withBaseUrl("https://flix.dev");

    // Sliding window: at most 2 requests per 1000ms window.
    run {
        println("--- Sliding window ---");
        let urls = List#{"/a", "/b", "/c", "/d"};
        foreach (url <- urls) {
            match Http.get(url) {
                case Ok(resp) => println("${url} -> ${HttpResponse.status(resp)}")
                case Err(err) => println("${url} -> ${err}")
            }
        }
    } with Http.withSlidingWindow(maxRequests = 2, window = seconds(1))
      with Http.withBaseUrl("https://flix.dev")

Composing Middleware

Middleware compose by stacking with clauses. Each with wraps the preceding block, so the outermost handler runs first. Here is an example that stacks base URL, default headers, retry, circuit breaker, rate limiting, and logging:

use Net.Http
use Net.Retry
use Net.HttpResponse
use Time.Clock
use Time.Duration.{milliseconds, seconds}

def main(): Unit \ { Clock, Http, Logger, IO } =
    let defaultHeaders = Map#{
        "Accept"        => List#{"application/json"},
        "Authorization" => List#{"Bearer tok123"}
    };
    run {
        let urls = List#{"/api/users", "/api/posts"};
        foreach (url <- urls) {
            match Http.get(url) {
                case Ok(resp) => println("${url} -> ${HttpResponse.status(resp)}")
                case Err(err) => println("${url} -> ${err}")
            }
        };
        match Http.get("https://notfound.flix.dev/") {
            case Ok(resp) => println("notfound -> ${HttpResponse.status(resp)}")
            case Err(err) => println("notfound -> ${err}")
        }
    } with Http.withBaseUrl("https://flix.dev")
      with Http.withDefaultHeaders(defaultHeaders)
      with Http.withRetry(Retry.linear(maxRetries = 2, delay = milliseconds(100)))
      with Http.withCircuitBreaker(failureThreshold = 3, cooldown = seconds(5))
      with Http.withSlidingWindow(maxRequests = 2, window = seconds(1))
      with Http.withLogging

The Http, Logger, and Clock effects all have default handlers, so they are handled automatically when they appear in the type signature of main.

Note: The order of with clauses matters. The outermost handler (listed last) wraps all inner handlers. In the example above, withLogging is outermost, so it sees every HTTP request — including retries and circuit-breaker probes. If we moved withLogging before withRetry, it would only see the original requests, not the retries. When composing middleware, think about which layer should observe which requests.

Logger

Flix provides Logger as a library effect for structured logging. The Logger effect has a default handler, so no explicit runWithIO call is needed in main. The key module is Logger.

The Logger Effect

The Logger effect has a single operation that logs a message at a given severity:

pub eff Logger {
    /// Logs the given message `m` at the given severity `s`.
    def log(s: Severity, m: RichString): Unit
}

The Severity enum defines five levels, from lowest to highest:

pub enum Severity with Eq, Order, ToString {
    case Trace
    case Debug
    case Info
    case Warn
    case Fatal
}

The Logger Module

The Logger module provides convenience functions:

mod Logger {
    /// Logs the message `m` at the Trace level.
    def trace(m: a): Unit \ Logger with Formattable[a]

    /// Logs the message `m` at the Debug level.
    def debug(m: a): Unit \ Logger with Formattable[a]

    /// Logs the message `m` at the Info level.
    def info(m: a): Unit \ Logger with Formattable[a]

    /// Logs the message `m` at the Warn level.
    def warn(m: a): Unit \ Logger with Formattable[a]

    /// Logs the message `m` at the Fatal level.
    def fatal(m: a): Unit \ Logger with Formattable[a]

Note: The logging functions accept any type that implements the Formattable trait. Most standard types (String, Int32, Bool, etc.) implement Formattable, so plain values can be logged directly. The trait converts values into RichString, which supports styled terminal output (colors, bold, etc.).

Logging Messages

The convenience functions accept any value that implements Formattable:

def main(): Unit \ { Logger } =
    Logger.info("Application started");
    Logger.debug("Loading configuration...");
    Logger.warn("Cache size exceeds threshold");
    Logger.fatal("Unrecoverable error")

The default handler prints each message to standard output with a colored severity prefix, for example: [Info] Application started.

Process

Flix provides Process as a library effect for spawning and managing OS processes. The Process effect has a default handler, so no explicit runWithIO call is needed in main. The key module is Sys.Process.

The Process Effect

The Process effect supports spawning processes, accessing their I/O streams, and waiting for completion:

pub eff Process {
    /// Executes `cmd` with `args`, working directory `cwd`, and environment `env`.
    def execWithCwdAndEnv(cmd: String, args: List[String],
        cwd: Option[String], env: Map[String, String]):
        Result[IoError, ProcessHandle]

    /// Returns the exit value of the process `ph`.
    def exitValue(ph: ProcessHandle): Result[IoError, Int32]

    /// Returns whether the process `ph` is alive.
    def isAlive(ph: ProcessHandle): Result[IoError, Bool]

    /// Returns the PID of the process `ph`.
    def pid(ph: ProcessHandle): Result[IoError, Int64]

    /// Returns the stdin stream of the process `ph`.
    def stdin(ph: ProcessHandle): Result[IoError, StdIn]

    /// Returns the stdout stream of the process `ph`.
    def stdout(ph: ProcessHandle): Result[IoError, StdOut]

    /// Returns the stderr stream of the process `ph`.
    def stderr(ph: ProcessHandle): Result[IoError, StdErr]

    /// Stops the process `ph`.
    def stop(ph: ProcessHandle): Result[IoError, Unit]

    /// Waits for the process `ph` to finish and returns its exit value.
    def waitFor(ph: ProcessHandle): Result[IoError, Int32]

    /// Waits at most `time` (in the given `tUnit`) for the process `ph` to finish.
    /// Returns `true` if the process exited, `false` if the timeout elapsed.
    def waitForTimeout(ph: ProcessHandle, time: Int64, tUnit: TimeUnit):
        Result[IoError, Bool]
}

The Process Module

The S module provides convenience functions built on the Process effect:

mod Process {
    /// Executes the command `cmd` with the arguments `args`.
    def exec(cmd: String, args: List[String]):
        Result[IoError, ProcessHandle] \ Process

    /// Executes `cmd` with `args` and working directory `cwd`.
    def execWithCwd(cmd: String, args: List[String], cwd: Option[String]):
        Result[IoError, ProcessHandle] \ Process

    /// Executes `cmd` with `args` and environment variables `env`.
    def execWithEnv(cmd: String, args: List[String], env: Map[String, String]):
        Result[IoError, ProcessHandle] \ Process
}

Executing a Command

The simplest way to spawn an OS process is with Process.exec. It takes a command and a list of arguments, and returns a Result[IoError, ProcessHandle]:

use Sys.Process

def main(): Unit \ { Process, IO } =
    match Process.exec("java", "-version" :: Nil) {
        case Result.Ok(_)    => println("Process started successfully.")
        case Result.Err(err) => println("Unable to execute process: ${err}")
    }

Reading Process Output

After spawning a process, you can access its output streams with Process.stdout and Process.stderr. The returned StdOut and StdErr types implement Readable, so you can read bytes from them:

use Sys.Process

def main(): Unit \ { Process, IO } = region rc {
    match Process.exec("java", "-version" :: Nil) {
        case Result.Err(err) => println("exec failed: ${err}")
        case Result.Ok(ph)   =>
            match Process.stderr(ph) {
                case Result.Err(err) => println("stderr failed: ${err}")
                case Result.Ok(err)  =>
                    let buf = Array.repeat(rc, 1024, (0i8: Int8));
                    match Readable.read(buf, err) {
                        case Result.Err(e) => println("read failed: ${e}")
                        case Result.Ok(n)  => println("Read ${n} bytes from stderr.")
                    }
            }
    }
}

Note: java -version writes to stderr, not stdout.

Waiting for Completion

Use Process.waitFor to block until a process exits. It returns the exit code as an Int32:

use Sys.Process

def main(): Unit \ { Process, IO } =
    match Process.exec("java", "-version" :: Nil) {
        case Result.Err(err) => println("exec failed: ${err}")
        case Result.Ok(ph)   =>
            match Process.waitFor(ph) {
                case Result.Err(err) => println("waitFor failed: ${err}")
                case Result.Ok(code) => println("Process exited with code: ${code}")
            }
    }

Working Directory and Environment

Process.execWithCwd spawns a process with a specific working directory. Process.execWithEnv passes additional environment variables:

use Sys.Process

def main(): Unit \ { Process, IO } =
    match Process.execWithCwd("java", "-version" :: Nil, Some("/tmp")) {
        case Result.Ok(_)    => println("execWithCwd succeeded.")
        case Result.Err(err) => println("execWithCwd failed: ${err}")
    };
    match Process.execWithEnv("java", "-version" :: Nil, Map#{"MY_VAR" => "hello"}) {
        case Result.Ok(_)    => println("execWithEnv succeeded.")
        case Result.Err(err) => println("execWithEnv failed: ${err}")
    }

Random

Flix provides Random as a library effect for generating pseudorandom numbers. The Random effect has a default handler, so no explicit runWithIO call is needed in main. The key module is Math.Random.

The Random Effect

The Random effect has two operations:

pub eff Random {
    /// Returns a pseudorandom 64-bit floating-point number in [0.0, 1.0].
    def randomFloat64(): Float64

    /// Returns a pseudorandom 64-bit integer.
    def randomInt64(): Int64
}

Generating Random Values

The simplest use of Random is to generate a value and act on it:

use Math.Random

def main(): Unit \ { Random, IO } =
    let flip = Random.randomFloat64() > 0.5;
    if (flip)
        println("heads")
    else
        println("tails")

Because Random has a default handler, the effect is handled automatically with a fresh random seed.

Seeded Randomness

The runWithSeed handler uses a fixed seed so that every run produces the same sequence of random values. This is useful for reproducible tests and benchmarks:

use Math.Random

def main(): Unit \ IO =
    run {
        let a = Random.randomFloat64();
        let b = Random.randomFloat64();
        println("a = ${a}, b = ${b}")
    } with Random.runWithSeed(42i64)

Because a seeded random number generator is fully deterministic, runWithSeed eliminates the Random effect without introducing IO.

Sleep

Flix provides Sleep as a library effect for pausing the current thread. The Sleep effect has a default handler, so no explicit runWithIO call is needed in main. The key module is Time.Sleep.

The Sleep Effect

The Sleep effect has a single operation:

pub eff Sleep {
    /// Sleeps the current thread for the given duration `d`.
    def sleep(d: Duration): Unit
}

Durations are created with helpers from the Time.Duration module, such as seconds, milliseconds, minutes, and so on.

Basic Sleep

The simplest use of Sleep is to pause for a fixed duration:

use Time.Duration.seconds
use Time.Sleep

def main(): Unit \ { Sleep, IO } =
    println("Going to sleep...");
    Sleep.sleep(seconds(1));
    println("Woke up!")

No-Op Sleep

The withNoOp handler skips all sleeps, which is useful for testing code that contains delays without actually waiting:

use Time.Duration.seconds
use Time.Sleep

def main(): Unit \ IO =
    run {
        println("Going to sleep...");
        Sleep.sleep(seconds(10));
        println("Woke up instantly!")
    } with Sleep.withNoOp

Because withNoOp fully handles the Sleep effect, the result type no longer includes Sleep.

Middleware

The Time.Sleep module provides several middleware handlers that intercept and transform sleep durations before forwarding to the underlying Sleep effect. Middleware re-raises Sleep, so multiple layers can be composed.

For example, withMaxSleep caps each sleep to a maximum and withLogging logs each duration:

use Time.Duration.{milliseconds, seconds}
use Time.Sleep

def main(): Unit \ { Logger, Sleep, IO } =
    run {
        println("Sleeping for 2 seconds (capped to 500ms)...");
        Sleep.sleep(seconds(2));
        println("Done!")
    } with Sleep.withMaxSleep(milliseconds(500))
      with Sleep.withLogging

Composing Middleware

Because each middleware re-raises Sleep, they stack naturally. The following example adds ±20% random jitter to each sleep and logs the resulting durations:

use Math.Random
use Time.Duration.{seconds}
use Time.Sleep

/// Composes `withJitter` and `withLogging` to add ±20% random jitter
/// to sleep durations and log each sleep via the `Logger` effect.
def main(): Unit \ { Logger, Random, Sleep, IO } =
    run {
        println("Sleeping 3 times with ±20% jitter...");
        Sleep.sleep(seconds(1));
        Sleep.sleep(seconds(2));
        Sleep.sleep(seconds(3));
        println("Done!")
    } with Sleep.withJitter(0.2)
      with Sleep.withLogging

The order matters: withJitter intercepts the original durations, applies jitter, and re-raises Sleep. The withLogging handler then sees the jittered durations.

Modules

Flix supports hierarchical modules as known from many other programming languages.

Declaring and Using Modules

We declare modules using the mod keyword followed by the namespace and name of the module.

For example, we can declare a module:

mod Math {
    pub def sum(x: Int32, y: Int32): Int32 = x + y
}

Here we have declared a module called Math with a function called sum inside it. We can refer to the sum function, from outside of its module, using its fully-qualified name:

def main(): Unit \ IO = 
    let result = Math.sum(123, 456);
    println(result)

Alternatively, we can bring the sum function into local scope with use:

def main(): Unit \ IO = 
    use Math.sum;
    let result = sum(123, 456);
    println(result)

Using Multiple Declarations from a Module

If we have multiple declarations in a module:

mod Math {
    pub def sum(x: Int32, y: Int32): Int32 = x + y
    pub def mul(x: Int32, y: Int32): Int32 = x * y
}

We can, of course, use each declaration:

use Math.sum;
use Math.mul;

def main(): Unit \ IO =
    mul(42, 84) |> sum(21) |> println

but a shorter way is to group the uses together into one:

use Math.{sum, mul};

def main(): Unit \ IO =
    mul(42, 84) |> sum(21) |> println

Note: Flix does not support wildcard uses since they can lead to subtle bugs.

Avoiding Name Clashes with Renaming

We can use renaming to avoid name clashes between identically named declarations.

For example, if we have two modules:

mod A {
    pub def concat(x: String, y: String): String = x + y
}

mod B {
    pub def concat(xs: List[Int32], ys: List[Int32]): List[Int32] = xs ::: ys
}

We can then use each concat function under a unique name. For example:

use A.{concat => concatStrings}
use B.{concat => concatLists}

def main(): Unit \ IO =
    concatStrings("Hello", " World!") |> println

While this feature is powerful, in many cases using a fully-qualified name might be more appropriate.

Modules and Enums

We can define an enum inside a module. For example:

mod Zoo {
    pub enum Animal {
        case Cat,
        case Dog,
        case Fox
    }
}

Here the Zoo module contains an enum type named Animal which has three cases: Cat, Dog, and Fox.

We can access the type and the cases using their fully-qualified names:

def says(a: Zoo.Animal): String = match a {
    case Zoo.Animal.Cat => "Meow"
    case Zoo.Animal.Dog => "Woof"
    case Zoo.Animal.Fox => "Roar"
}

def main(): Unit \ IO = 
    println("A cat says ${says(Zoo.Animal.Cat)}!")

Alternatively, we can use both the Animal type and its cases:

use Zoo.Animal
use Zoo.Animal.Cat
use Zoo.Animal.Dog
use Zoo.Animal.Fox

def says(a: Animal): String = match a {
    case Animal.Cat => "Meow"
    case Animal.Dog => "Woof"
    case Animal.Fox => "Roar"
}

def main(): Unit \ IO = 
    println("A cat says ${says(Cat)}!")

Note that use Zoo.Animal brings the Animal type into scope, whereas use Zoo.Animal.Cat brings the Cat case into scope.

Modules and Trait

We can also define a trait inside a module. The mechanism is similar to enums inside modules.

For example, we can write:

mod Zoo {
    pub trait Speakable[t] {
        pub def say(x: t): String
    }
}

enum Animal with ToString {
    case Cat,
    case Dog,
    case Fox
}

instance Zoo.Speakable[Animal] {
    pub def say(a: Animal): String = match a {
        case Cat => "Meow"
        case Dog => "Woof"
        case Fox => "Roar"
    }
}

We can use fully-qualified names to write:

def speak(x: t): Unit \ IO with Zoo.Speakable[t], ToString[t] = 
    println("A ${x} says ${Zoo.Speakable.say(x)}!")

def main(): Unit \ IO = 
    speak(Animal.Cat)

Or we can use the Zoo.Speakable trait and the Zoo.Speakable.say function:

use Zoo.Speakable
use Zoo.Speakable.say

def speak(x: t): Unit \ IO with Speakable[t], ToString[t] = 
    println("A ${x} says ${say(x)}!")

Declaring Modules

As we have already seen, modules can be declared using the mod keyword:

mod Museum {
    // ... members ...
}

We can nest modules inside other modules:

mod Museum {
    mod Entrance {
        pub def buyTicket(): Unit \ IO = 
            println("Museum.Entrance.buyTicket() was called.")
    }

    mod Restaurant {
        pub def buyMeal(): Unit \ IO = 
            println("Museum.Restaurant.buyMeal() was called.")
    }

    mod Giftshop {
        pub def buyGift(): Unit \ IO = 
            println("Museum.Giftshop.buyGift() was called.")
    }
}

We can call these methods as follows:

def main(): Unit \ IO = 
    Museum.Entrance.buyTicket();
    Museum.Restaurant.buyMeal();
    Museum.Giftshop.buyGift()

Or alternatively as follows:

use Museum.Entrance.buyTicket;
use Museum.Restaurant.buyMeal;
use Museum.Giftshop.buyGift;
def main(): Unit \ IO = 
    buyTicket();
    buyMeal();
    buyGift()

Accessibility

A module member m declared in module A is accessible from another module B if:

• the member m is declared as public (pub).
• the module B is a sub-module of A.

For example, the following is allowed:

mod A {
    mod B {
       pub def g(): Unit \ IO = A.f() // OK
    }

    def f(): Unit \ IO = println("A.f() was called.")
}

Here f is private to the module A. However, since B is a sub-module of A can access f from inside B. On the other hand, the following is not allowed:

mod A {
    mod B {
       def g(): Unit \ IO = println("A.B.g() was called.")
    }

    pub def f(): Unit \ IO = A.B.g() // NOT OK
}

because g is private to B.

Using Modules

As we have already seen, the use construct brings members of a module into local scope.

For example, given the program:

mod A {
    mod B {
        pub enum Color {
            case Red, Green, Blue
        }

        pub type alias Hue = Color 

        pub def isWarm(c: Color): Bool = 
            match c {
                case Color.Red    => true
                case Color.Green  => false
                case Color.Blue   => false
            }

    }
}

All of the following uses are meaningful:

use A.B.Color 
use A.B.Color.{Red, Green, Blue}
use A.B.Hue
use A.B.isWarm 

All Kinds of Uses

Flix supports several kinds of uses, including:

• A qualified use of a name: use A.B.Color.
• A qualified use of multiple names: use A.B.Color.{Red, Green, Blue}.
• A qualified use with rename: use A.B.Color => AColor.
• A qualified use with multiple renames: use A.B.Color.{Red => R, Green => G, Blue => B}.

Note: Flix does not support wildcard.

Where can Uses Occur?

Flix supports uses in two places:

• Inside modules.
• Inside functions.

For example:

mod A {
    use Chain
    use Chain.Empty
    use Chain.Chain
    use Int32.max

    pub def maxValue(c: Chain[Int32]): Int32 = 
        match c {
            case Empty       => 0
            case One(x)      => x
            case Chain(x, y) => max(maxValue(x), maxValue(y))
        }
}

which can also be written as:

mod A {
    use Chain

    pub def maxValue(c: Chain[Int32]): Int32 = 
        use Chain.Empty;
        use Chain.Chain;
        use Int32.max;
        match c {
            case Empty       => 0
            case One(x)      => x
            case Chain(x, y) => max(maxValue(x), maxValue(y))
        }
}

Note the use of semicolons when inside an expression.

Default Uses

In Flix, a few built-in constructors are always in scope:

• List.Nil and List.Cons.
• Result.Ok and Result.Err.

Companion Modules

In Flix every enum and trait declaration is associated with a companion module.

Enum Companions

When we declare an enum, its type and cases are automatically available inside its companion module. For example, we can write:

enum Color {
    case Red,
    case Green,
    case Blue
}

mod Color {
    pub def isWarm(c: Color): Bool = match c {
        case Red    => true
        case Green  => false
        case Blue   => false
    }
}

Here the Color type and the Red, Green, and Blue cases are automatically in scope within the companion Color module.

Trait Companions

Every trait declaration also gives rise to a companion module.

For example, we can define a trait Addable for types whose elements can be added:

trait Addable[t] {
    pub def add(x: t, y: t): t
}

The Addable trait implicitly introduces a companion module Addable. We typically use the companion module to store functionality that is related to the trait.

For example, we could have:

mod Addable {
    pub def add3(x: t, y: t, z: t): t with Addable[t] = add(add(x, y), z)
}

When accessing a member of Addable, Flix will automatically look in both the trait declaration and its companion module. Consequently, Addable.add refers to the trait member add whereas Addable.add3 refers to the function inside the Addable module. Note that the add signature is in the scope of the Addable module.

We should be aware that functions defined in the companion module of a trait cannot be redefined by instances of the associated trait. Thus we should only put members into the companion namespace when we do not intend to redefine them later.

Traits

Traits, also known as type classes, support abstraction and modularity. The Flix trait system is similar to that of Haskell and Rust, but not identical. Traits in Flix support associated types, associated effects, and higher-kinded types.

We illustrate traits with an example.

We can define equality on Option[Int32] as follows:

def equals(x: Option[Int32], y: Option[Int32]): Bool = 
    match (x, y) {
        case (None, None)         => true
        case (Some(v1), Some(v2)) => v1 == v2
        case _                    => false
    }

We can also define equality on List[Int32] as follows:

def equals(x: List[Int32], y: List[Int32]): Bool = 
    match (x, y) {
        case (Nil, Nil)           => true
        case (v1 :: xs, v2 :: ys) => v1 == v2 and equals(xs, ys)
        case _                    => false
    }

But what if we wanted a common abstraction for data types which support equality?

Here we can use traits. We can define an Equatable trait:

trait Equatable[t] {
    pub def equals(x: t, y: t): Bool
}

which has a single equals trait signature. The trait is polymorphic over the type parameter t which means that we can implement Equatable for both Option[t] and List[t]:

instance Equatable[Option[t]] with Equatable[t] {
    pub def equals(x: Option[t], y: Option[t]): Bool = 
        match (x, y) {
            case (None, None)         => true
            case (Some(v1), Some(v2)) => Equatable.equals(v1, v2)
            case _                    => false
        }
}

Notice that we did not implement Equatable for Option[Int32], but instead for any Option[t] as long as t itself is equatable. Moreover, instead of comparing v1 and v2 directly using ==, we call Equatable.equals on them.

We can also implement Equatable for List[t]:

instance Equatable[List[t]] with Equatable[t] {
    pub def equals(x: List[t], y: List[t]): Bool = 
        use Equatable.equals;
        match (x, y) {
            case (Nil, Nil)           => true
            case (v1 :: xs, v2 :: ys) => equals(v1, v2) and equals(xs, ys)
            case _                    => false
        }
}

Assuming we also implement Equatable for Int32, we can use Equatable to compute whether two Option[Int32] values are equal. But we can also compute if two Option[List[Int32]] values are equal! This demonstrates the power of abstraction: We have implemented instances for Option[t] and List[t] and we can now reuse these instances everywhere.

We can use our newly defined Equatable trait to write polymorphic functions.

For example, we can define a function to compute if an element occurs in a list:

def memberOf(x: t, l: List[t]): Bool with Equatable[t] = 
    match l {
        case Nil     => false
        case y :: ys => Equatable.equals(x, y) or memberOf(x, ys)
    }

We can use memberOf for a list of any type, as the element type implements Equatable.

Note: In the Flix Standard Library the Equatable trait is called Eq. Moreover, the == operator is syntactic sugar for the trait signature Eq.eq.

Sealed Traits

We can declare a trait as sealed to restrict who can implement the trait.

For example:

mod Zoo {
    sealed trait Animal[a] {
        pub def isMammal(x: a): Bool
    }

    instance Animal[Giraffe] {
        pub def isMammal(_: Giraffe): Bool = true
    }

    instance Animal[Penguin] {
        pub def isMammal(_: Penguin): Bool = false
    }

    pub enum Giraffe
    pub enum Penguin
}

Here we can implement instances for Animal and Giraffe because they occur in the same module as the Animal trait. But we cannot implement Animal from outside the Zoo module. If we try:

mod Lake {
    pub enum Swan

    instance Zoo.Animal[Swan] {
        pub def isMammal(_: Swan): Bool = false
    }
}

then Flix reports:

❌ -- Resolution Error -------------------------------------------------- 

>> Trait 'Zoo.Animal' is sealed from the module 'Lake'.

21 |     instance Zoo.Animal[Swan] {
                  ^^^^^^^^^^
                  sealed trait.

Malformed Traits

A trait is not a C# or Java-style interface. Specifically:

• every trait must have exactly one type parameter, and
• every signature must mention that type parameter.

For example, the following trait is incorrect:

trait Animal[a] {
    pub def isMammal(x: a): Bool      // OK     -- mentions a.
    pub def numberOfGiraffes(): Int32 // NOT OK -- does not mention a.
}

If we compile the above trait, Flix reports:

❌ -- Resolution Error -------------------------------------------------- 

>> Unexpected signature 'numberOfGiraffes' which does not mention the type 
>> variable of the trait.

7 |     pub def numberOfGiraffes(): Int32 
                ^^^^^^^^^^^
                unexpected signature.

The problem is that the signature for numberOfGiraffes does not mention the type parameter a.

Complex Instances

A trait instance must be defined on:

• exactly one type constructor —
• that is applied to zero or more distinct type variables.

For example, given the Equatable trait from before:

trait Equatable[t] {
    pub def equals(x: t, y: t): Bool
}

We can implement instances for e.g.:

• Option[a]
• List[a]
• (a, b)

but we cannot implement instances for e.g.:

• Option[Int32]
• List[String]
• (a, Bool)
• Map[Int32, v]

If we try to implement an instance for e.g. List[Int32] Flix reports:

❌ -- Instance Error -------------------------------------------------- 

>> Complex instance type 'List[Int32]' in 'Equatable'.

6 | instance Equatable[List[Int32]] {
             ^^^^^^^^^
             complex instance type

An instance type must be a type constructor applied to zero or more 
distinct type variables.

Overlapping Instances

We cannot implement two instances of of the same trait for overlapping types.

For example, if we try to implement two instances of Equatable for List[t]:

instance Equatable[List[t]] {
    pub def equals(x: List[t], y: List[t]): Bool = ???
}

instance Equatable[List[t]] {
    pub def equals(x: List[t], y: List[t]): Bool = ???
}

then Flix reports:

❌ -- Instance Error -------------------------------------------------- 

>> Overlapping instances for 'Equatable'.

1 | instance Equatable[List[t]] {
              ^^^^^^^^^
              the first instance was declared here.

4 | instance Equatable[List[t]] {
             ^^^^^^^^^
             the second instance was declared here.

Essential Traits

Practical programming in Flix requires knowledge of at least three traits: Eq, Order, and ToString.

The Eq Trait

The Eq trait captures when two values of a specific type are equal:

trait Eq[a] {

    ///
    /// Returns `true` if and only if `x` is equal to `y`.
    ///
    pub def eq(x: a, y: a): Bool

    // ... additional members omitted ...
}

To implement Eq, we only have to implement the eq function. When we implement eq we automatically get an implementation of Eq.neq.

The Order Trait

The Order trait captures when one value is smaller or equal to another value of the same type:

trait Order[a] with Eq[a] {

    ///
    /// Returns `Comparison.LessThan` if `x` < `y`, 
    /// `Equal` if `x` == `y` or 
    /// `Comparison.GreaterThan` if `x` > `y`.
    ///
    pub def compare(x: a, y: a): Comparison

    // ... additional members omitted ...
}

To implement the Order trait, we must implement the compare function which returns value of type Comparison. The Comparison data type is defined as:

enum Comparison {
    case LessThan
    case EqualTo
    case GreaterThan
}

When we implement compare, we automatically get implementations of Order.less, Order.lessThan, Order.greater, Order.greaterEqual, Order.max, and Order.min.

The ToString Trait

The ToString trait is used to obtain a string representation of a specific value:

trait ToString[a] {
    ///
    /// Returns a string representation of the given `x`.
    ///
    pub def toString(x: a): String
}

Flix uses the ToString trait in string interpolations.

For example, the interpolated string

"Good morning ${name}, it is ${hour} o'clock."

is actually syntactic sugar for the expression:

"Good morning " + ToString.toString(name) + ", it is " 
                + ToString.toString(hour) + " o'clock."

In the following subsection, we discuss how to automatically derive implementations of the Eq, Order, and ToString traits.

Automatic Derivation

Flix supports automatic derivation of several traits, including:

• Eq — to derive structural equality on the values of a type.
• Order — to derive a total ordering on the values of a type.
• ToString — to derive a human-readable string representation on the values of a type.
• Sendable — to enable the values of an (immutable) type to be sent over a channel.
• Coerce - to convert simple data types to their underlying representation.

Derivation of Eq and Order

We can automatically derive instances of the Eq and Order traits using the with clause in the enum declaration. For example:

enum Shape with Eq, Order {
    case Circle(Int32)
    case Square(Int32)
    case Rectangle(Int32, Int32)
}

The derived implementations are structural and rely on the order of the case declarations:

def main(): Unit \ IO = 
    println(Circle(123) == Circle(123)); // prints `true`.
    println(Circle(123) != Square(123)); // prints `true`.
    println(Circle(123) <= Circle(123)); // prints `true`.
    println(Circle(456) <= Square(123))  // prints `true`.

Note: Automatic derivation of Eq and Order requires that the inner types of the enum implement Eq and Order themselves.

Derivation of ToString

We can also automatically derive ToString instances:

enum Shape with ToString {
    case Circle(Int32)
    case Square(Int32)
    case Rectangle(Int32, Int32)
}

Then we can take advantage of string interpolation and write:

def main(): Unit \ IO = 
    let c = Circle(123);
    let s = Square(123);
    let r = Rectangle(123, 456);
    println("A ${c}, ${s}, and ${r} walk into a bar.")

which prints:

A Circle(123), Square(123), and Rectangle(123, 456) walk into a bar.

Derivation of Sendable

We can automatically derive implementations of the Sendable trait (which allow values of a specific type to be sent over a channel). For example:

enum Shape with Sendable, ToString {
    case Circle(Int32)
}

def main(): Unit \ IO = 
    region rc {
        let (tx, rx) = Channel.buffered(rc, 10);
        Channel.send(Circle(123), tx); // OK, since Shape is Sendable.
        println(Channel.recv(rx))
    }

We cannot derive Sendable for types that rely on scoped mutable memory. For example, if we try:

enum Shape[r: Region] with Sendable {
    case Circle(Array[Int32, r])
}

The Flix compiler emits a compiler error:

❌ -- Safety Error --------------------------------------

>> Cannot derive 'Sendable' for type Shape[b27587945]

Because it takes a type parameter of kind 'Region'.

1 | enum Shape[r: Region] with Sendable {
                               ^^^^^^^^
                               unable to derive Sendable.

This is because mutable data is not safe to share between threads.

Derivation of Coerce

We can automatically derive implementations of the Coerce trait. The Coerce trait converts a simple (one-case) data type to its underlying implementation.

enum Shape with Coerce {
    case Circle(Int32)
}

def main(): Unit \ IO =
    let c = Circle(123);
    println("The radius is ${coerce(c)}")

We cannot derive Coerce for an enum with more than one case. For example, if we try:

enum Shape with Coerce {
    case Circle(Int32)
    case Square(Int32)
}

The Flix compiler emits a compiler error:

❌ -- Derivation Error --------------------------------------------------

>> Cannot derive 'Coerce' for the non-singleton enum 'Shape'.

1 | enum Shape with Coerce {
                    ^^^^^^
                    illegal derivation

'Coerce' can only be derived for enums with exactly one case.

Associated Types

An associated type is a type member of a trait that is specified by each trait instance. Associated types are often considered a more natural alternative to multi-parameter type classes.

We illustrate associated types with an example.

We can define a trait for types that can be added:

trait Addable[t] {
    pub def add(x: t, y: t): t
}

We can implement multiple instances of the Addable trait for types such as floating-point numbers, integers, and strings. For example, here is the instance for Int32:

instance Addable[Int32] {
    pub def add(x: Int32, y: Int32): Int32 = x + y
}

and here is one for String:

instance Addable[String] {
    pub def add(x: String, y: String): String = "${x}${y}"
}

But what if we wanted to add an element to a set?

Intuitively, we would like to write:

instance Addable[Set[a]] with Order[a] {
    pub def add(s: Set[a], x: a): Set[a] = Set.insert(x, s)
}

But the signature of add does not match the signature declared in Addable.

We can overcome this problem and increase the flexibility of Addable with an associated type:

trait Addable[t] {
    type Rhs
    pub def add(x: t, y: Addable.Rhs[t]): t
}

The Addable trait now has an associated type called Rhs. We refer to it as Addable.Rhs[t] as seen in the signature of add. Whenever we declare an instance of Addable, we must specify the associated type.

We can still implement instances for integers and strings, as before. For example:

instance Addable[Int32] {
    type Rhs = Int32
    pub def add(x: Int32, y: Int32): Int32 = x + y
}

But we can also implement an instance that allows adding an element to a set:

instance Addable[Set[a]] with Order[a] {
    type Rhs = a
    pub def add(s: Set[a], x: a): Set[a] = Set.insert(x, s)
}

The important point is that each trait instance specifies the associated type.

We might wonder if we can specify two instances for Set[a]: (a) one for adding an element to a set, as above, and (b) one for adding two sets:

instance Addable[Set[a]] with Order[a] {
    type Rhs = Set[a]
    pub def add(x: Set[a], y: Set[a]): Set[a] = Set.union(x, y)

}

But while each instance is valid on its own, we cannot have both:

❌ -- Instance Error -------------------------------------------------- 

>> Overlapping instances for 'Addable'.

...

If we had such overlapping instances, an expression like Addable.add(Set#{}, Set#{}) would become ambiguous: Are we adding two sets? Or are we adding the empty set to a set?

Example: A ForEach Trait

We can use associated types to define a trait for collections that have a forEach function:

trait ForEach[t] {
    type Elm
    pub def forEach(f: ForEach.Elm[t] -> Unit \ ef, x: t): Unit \ ef
}

Here t is the type of the collection and the associated type Elm is the type of its elements. We can implement several instances for ForEach. For example, we can implement an instance for List[a]:

instance ForEach[List[a]] {
    type Elm = a
    pub def forEach(f: a -> Unit \ ef, x: List[a]): Unit \ ef = List.forEach(f, x)
}

We can also implement an instance for Map[k, v]:

instance ForEach[Map[k, v]] {
    type Elm = (k, v)
    pub def forEach(f: ((k, v)) -> Unit \ ef, x: Map[k, v]): Unit \ ef = 
        Map.forEach(k -> v -> f((k, v)), x)
}

What is interesting and useful is that we can define the element type to be key-value pairs. We need extra parentheses around the argument to f because we want it to take a pair.

We can implement an instance for String where we can iterate through each individual character:

instance ForEach[String] {
    type Elm = Char
    pub def forEach(f: Char -> Unit \ ef, x: String): Unit \ ef = 
        x |> String.toList |> List.forEach(f)
}

Example: A Collection Trait

As another example, we can define a trait for collections:

trait Collection[t] {
    type Elm
    pub def empty(): t
    pub def insert(x: Collection.Elm[t], c: t): t
    pub def toList(c: t): List[Collection.Elm[t]]
}

Here t is the type of the collection and Elm is the type of its elements. Every collection must support three operations: empty, insert, and toList.

We can implement an instance of Collection for Vector[a]:

instance Collection[Vector[a]] {
    type Elm = a
    pub def empty(): Vector[a] = Vector.empty()
    pub def insert(x: a, c: Vector[a]): Vector[a] = Vector.append(c, Vector#{x})
    pub def toList(c: Vector[a]): List[a] = Vector.toList(c)
}

And we can implement an instance of Collection for Set[a]:

instance Collection[Set[a]] with Order[a] {
    type Elm = a
    pub def empty(): Set[a] = Set.empty()
    pub def insert(x: a, c: Set[a]): Set[a] = Set.insert(x, c)
    pub def toList(c: Set[a]): List[a] = Set.toList(c)
}

Equality Constraints

We sometimes want to write polymorphic functions where we restrict an associated type.

For example, returning to the example of the Collection trait, we can write a function where we require that the element type is an Int32. This allows us to write a sum function:

def sum(c: t): Int32 with Collection[t] where Collection.Elm[t] ~ Int32 = 
    Collection.toList(c) |> List.sum

Here the where clause contains a list of type equality constraints. Specifically, the equality constraint Collection.Elm[t] ~ Int32 assert that sum can be used with any type t for which there is an instance of Collection as long as the element type of that instance is equal to Int32. This restriction ensures that the elements of the collection are integers and allows us to call List.sum.

Default Types

We can define a default type for an associated type.

Returning to Addable, we can define the associated type Rhs with t as its default:

trait Addable[t] {
    type Rhs = t  // Associated type with default type.
    pub def add(x: t, y: Addable.Rhs[t]): t
}

Here we specify that if Rhs is not defined by an instance implementation then it defaults to t. The upshot is that we can define an instance for Int32:

instance Addable[Int32] {
    pub def add(x: Int32, y: Int32): Int32 = x + y
}

without having to explicit define type Rhs = Int32.

Associated Effects

We have seen how associated types increase the flexibility of traits by allowing each instance to specify concrete types for the associated types. Associated effects work in the same manner, but concern effects.

We motivate the need for associated effects with a simple example.

We can define a trait for types that can be divded:

trait Dividable[t] {
    pub def div(x: t, y: t): t
}

and we can implement the trait for e.g. Float32 and Int32:

instance Dividable[Float32] {
    pub def div(x: Float32, y: Float32): Float32 = x / y
}

instance Dividable[Int32] {
    pub def div(x: Int32, y: Int32): Int32 = x / y
}

But what about division-by-zero? Assume we want to raise an exception and have it tracked by the type and effect system. We would like to write:

pub eff DivByZero {
    pub def raise(): Void
}

instance Dividable[Int32] {
    pub def div(x: Int32, y: Int32): Int32 \ DivByZero = 
        if (y == 0) DivByZero.raise() else x / y
}

But unfortunately this does not quite work:

❌ -- Type Error --------------------------------------------------

>> Mismatched signature 'div' required by 'Dividable'.

14 |     pub def div(x: Int32, y: Int32): Int32 \ DivByZero = 
                 ^^^
...

The problem, as the compiler explains, is that the definition of div in the trait Dividable is declared as pure. Hence we are not allowed to raise an exception. We could change the signature of Dividable.div, but that would be problematic for the Float32 instance, because division-by-zero returns NaN and does not raise an exception.

The solution is to use an associated effect: then the instance for Int32 can specify that a DivByZero exception may be raised whereas the instance for Float32 can be pure. We add an associated effect Aef to Dividable:

trait Dividable[t] {
    type Aef: Eff
    pub def div(x: t, y: t): t \ Dividable.Aef[t]
}

and we re-implement the instances for Float32 and Int32:

instance Dividable[Float32] {
    type Aef = { Pure } // No exception, div-by-zero yields NaN.
    pub def div(x: Float32, y: Float32): Float32 = x / y
}

instance Dividable[Int32] {
    type Aef = { DivByZero }
    pub def div(x: Int32, y: Int32): Int32 \ DivByZero = 
        if (y == 0) DivByZero.raise() else x / y
}

Associated Effects and Regions

We often want to use associated effects in combination with regions.

Assume we have the ForEach trait from before:

trait ForEach[t] {
    type Elm
    pub def forEach(f: ForEach.Elm[t] -> Unit \ ef, x: t): Unit \ ef
}

As we have seen, we can implement it for e.g. List[t] but also Map[k, v]. But what if we wanted to implement it for e.g. MutList[t, r] or MutSet[t, r]. We can try:

instance ForEach[MutList[t, r]] {
    type Elm = t
    pub def forEach(f: t -> Unit \ ef, x: MutList[t, r]): Unit \ ef = 
        MutList.forEach(f, x)
}

But Flix reports:

❌ -- Type Error -------------------------------------------------- 

>> Unable to unify the effect formulas: 'ef' and 'ef + r'.

9 |         MutList.forEach(f, x)
            ^^^^^^^^^^^^^^^^^^^^^
            mismatched effect formulas.

The problem is that MutList.forEach has an effect in the region r, but the signature of forEach in the trait only permits the ef effect from the function f.

We can solve the problem by extending the ForEach trait with an associated effect:

trait ForEach[t] {
    type Elm
    type Aef: Eff
    pub def forEach(f: ForEach.Elm[t] -> Unit \ ef, x: t): Unit \ ef + ForEach.Aef[t]
}

We must specify that Aef is an effect with the kind annotation Aef: Eff. If we don’t specify the kind then it defaults to Type which is not what we want here.

With the updated ForEach trait, we can implement it for both List[t] and MutList[t]:

instance ForEach[List[t]] {
    type Elm = t
    type Aef = { Pure }
    pub def forEach(f: t -> Unit \ ef, x: List[t]): Unit \ ef = List.forEach(f, x)
}

and

instance ForEach[MutList[t, r]] {
    type Elm = t
    type Aef = { r }
    pub def forEach(f: t -> Unit \ ef, x: MutList[t, r]): Unit \ ef + r = 
        MutList.forEach(f, x)
}

Notice how the implementation for List[t] specifies that the associated effect is pure, whereas the implementation for MutList[t, r] specifies that there is a heap effect in region r.

Higher-Kinded Types

Flix supports higher-kinded types, hence traits can abstract over type constructors.

For example, we can write a trait that capture iteration over any collection of the shape t[a] where t is a type constructor of kind Type -> Type and a is the element type of kind Type:

trait ForEach[t: Type -> Type] {
    pub def forEach(f: a -> Unit \ ef, x: t[a]): Unit \ ef
}

To use higher-kinded types Flix requires us to provide kind annotations, i.e. we had to write t: Type -> Type to inform Flix that ForEach abstracts over type constructors.

We can implement an instance of the ForEach trait for Option:

instance ForEach[Option] {
    pub def forEach(f: a -> Unit \ ef, o: Option[a]): Unit \ ef = match o {
        case None    => ()
        case Some(x) => f(x)
    }
}

and we can implement an instance for List:

instance ForEach[List] {
    pub def forEach(f: a -> Unit \ ef, l: List[a]): Unit \ ef = List.forEach(f, l)
}

The Flix Kinds

Flix supports the following kinds:

• Type: The kind of Flix types.
  • e.g. Int32, String, and List[Int32].
• RecordRow: The kind of rows used in records
  • e.g. in {x = Int32, y = Int32 | r} the type variable r has kind RecordRow.
• SchemaRow: The kind of rows used in first-class Datalog constraints
  • e.g. in #{P(Int32, Int32) | r} the type variable r has kind SchemaRow.

Flix can usually infer kinds. For example, we can write:

def sum(r: {x = t, y = t | r}): t with Add[t] = r#x + r#y

and have the kinds of t: Type and r: RecordRow automatically inferred.

We can also explicitly specify them as follows:

def sum[t: Type, r: RecordRow](r: {x = t, y = t | r}): t with Add[t] = r#x + r#y

but this style is not considered idiomatic.

Flix requires explicit kind annotations in four situations:

• For type parameters of non-Type kind on enums.
• For type parameters of non-Type kind on type aliases.
• For type parameters of non-Type kind on traits.
• For type members of a non-Type kind in a trait.

The most common scenario where you will need a kind annotation is when you want a type parameter or type member to range over an effect.

Higher-Kinded Types vs. Associated Types

In practice higher-kinded types and associated types can be used to define similar abstractions.

For example, as we have seen, we can define the ForEach trait in two different ways:

With a higher-kinded type:

trait ForEach[t: Type -> Type] {
    pub def forEach(f: a -> Unit \ ef, x: t[a]): Unit \ ef
}

and with an associated type:

trait ForEach[t] {
    type Elm
    pub def forEach(f: ForEach.Elm[t] -> Unit \ ef, x: t): Unit \ ef
}

In the case of ForEach, the definition with an associated type is more flexible, since we can implement an instance for String with associated element type Char. However, higher-kinded types are still useful. For example, the Flix Standard Library defines the Functor trait as:

trait Functor[m : Type -> Type] {
    pub def map(f: a -> b \ ef, x: m[a]): m[b] \ ef
}

Notably the kind of m ensures that every Functor implementation is structure preserving. That is, we know that when we map over e.g. an Option[a] then we get back an Option[b].

Structured Concurrency

Flix supports CSP-style concurrency with channels and processes inspired by Go and Rust.

Spawning Processes

We can spawn a process with the spawn keyword:

def main(): Unit \ IO = region rc {
    spawn println("Hello from thread") @ rc;
    println("Hello from main")
}

Spawned processes are always associated with a region; the region will not exit until all the processes associated with it have completed:

def slowPrint(delay: Int32, message: String): Unit \ IO =
    Thread.sleep(Time.Duration.fromSeconds(delay));
    println(message)

def main(): Unit \ IO =
    region r1 {
        region r2 {
            spawn slowPrint(2, "Hello from r1") @ r1;
            spawn slowPrint(1, "Hello from r2") @ r2
        };
        println("r2 is now complete")
    };
    println("r1 is now complete")

This means that Flix supports structured concurrency; spawned processes have clearly defined entry and exit points.

Communicating with Channels

To communicate between processes we use channels. A channel allows two or more processes to exchange data by sending immutable messages to each other.

A channel comes in one of two variants: buffered or unbuffered. Channels are always associated with a region.

A buffered channel has a size, set at creation time, and can hold that many messages. If a process attempts to put a message into a buffered channel that is full, then the process is blocked until space becomes available. If, on the other hand, a process attempts to get a message from an empty channel, the process is blocked until a message is put into the channel.

An unbuffered channel works like a buffered channel of size zero; for a get and a put to happen both processes must rendezvous (block) until the message is passed from sender to receiver.

Here is an example of sending and receiving a message over a channel:

def main(): Int32 \ {Chan, NonDet, IO} = region rc {
    let (tx, rx) = Channel.unbuffered();
    spawn Channel.send(42, tx) @ rc;
    Channel.recv(rx)
}

Here the main function creates an unbuffered channel which returns Sender tx and a Receiver rx channels, spawns the send function, and waits for a message from the channel.

As the example shows, a channel consists of two end points: the Sender and the Receiver. As one would expect, messages can only be send using the Sender, and only received using the Receiver.

Selecting on Channels

We can use the select expression to receive a message from a collection of channels. For example:

def meow(tx: Sender[String]): Unit \ Chan =
    Channel.send("Meow!", tx)

def woof(tx: Sender[String]): Unit \ Chan =
    Channel.send("Woof!", tx)

def main(): Unit \ {Chan, NonDet, IO} = region rc {
    let (tx1, rx1) = Channel.buffered(1);
    let (tx2, rx2) = Channel.buffered(1);
    spawn meow(tx1) @ rc;
    spawn woof(tx2) @ rc;
    select {
        case m <- recv(rx1) => m
        case m <- recv(rx2) => m
    } |> println
}

Many important concurrency patterns such as producer-consumer and load balancers can be expressed using the select expression.

Selecting with Default

In some cases, we do not want to block until a message arrives, potentially waiting forever. Instead, we want to take some alternative action if no message is readily available. We can achieve this with a default case as shown below:

def main(): String \ {Chan, NonDet} = region rc {
    let (_, rx1) = Channel.buffered(1);
    let (_, rx2) = Channel.buffered(1);
    select {
        case _ <- recv(rx1) => "one"
        case _ <- recv(rx2) => "two"
        case _             => "default"
    }
}

Here a message is never sent to r1 nor r2. The select expression tries all cases, and if no channel is ready, it immediately selects the default case. Hence using a default case prevents the select expression from blocking forever.

Selecting with Timeouts

As an alternative to a default case, we can use tickers and timers to wait for pre-defined periods of time inside a select expression.

For example, here is a program that has a slow function that takes a minute to send a message on a channel, but the select expression relies on Channel.timeout to only wait 5 seconds before giving up:

def slow(tx: Sender[String]): Unit \ {Chan, IO} =
    Thread.sleep(Time.Duration.fromSeconds(60));
    Channel.send("I am very slow", tx)

def main(): Unit \ {Chan, NonDet, IO} = region rc {
    let (tx, rx) = Channel.buffered(1);
    spawn slow(tx) @ rc;
    let timeout = Channel.timeout(Time.Duration.fromSeconds(5));
    select {
        case m <- recv(rx)       => m
        case _ <- recv(timeout)  => "timeout"
    } |> println
}

This program prints the string "timeout" after five seconds.

The Effects of Channels

As you might have noticed, the effects Chan and NonDet shows up when using channels.

Any operation on channels has the Chan effect. This effect says that the program is either modifying or accessing the global state of channels.

The recv operation on a channel has the NonDet effect. This is because the value you receive will, in the general case, be non-deterministic, depending on the choices of the thread scheduler. Two threads might be ready to send a value on a channel at the same time, and it is up to the scheduler which one gets to send first.

Parallelism

We have seen how the spawn expression allows us to evaluate an expression in a new thread:

region rc {
    spawn (1 + 2) @ rc
}

This allows us to write concurrent and parallel programs using structured concurrency. The downside is that we must manually coordinate communication between threads using channels. If we want parallelism, but not concurrency, a more light-weight approach is to use the par-yield expression:

par (x <- e1; y <- e2; z <- e3)
    yield x + y + z

which evaluates e1, e2, and e3 in parallel and binds their results to x, y, and z.

We can use par-yield to write a parallel List.map function:

def parMap(f: a -> b, l: List[a]): List[b] = match l {
    case Nil     => Nil
    case x :: xs =>
        par (r <- f(x); rs <- parMap(f, xs))
            yield r :: rs
}

This function will evaluate f(x) and parMap(f, xs) in parallel.

Note: The par-yield construct only works with pure expressions.

If you want to run effectful operations in parallel, you must use explicit regions and threads.

Interoperability with Java

Flix is a Java Virtual Machine (JVM)-based programming language, hence:

• Flix programs compile to efficient JVM bytecode.
• Flix programs run on any Java Virtual Machine¹.
• Flix programs can call Java code.

Flix supports most Java features necessary for interoperability:

• Creating objects from classes
• Calling methods on classes and objects
• Reading and writing fields on classes and objects
• Anonymous extension of classes and interfaces
• Accessing inner classes
• Catching and throwing exceptions
• Boxing and unboxing of primitive values

Thus Flix programs can reuse the Java Class Library. In addition, the Flix package manager has Maven support.

Flix and Java share the same base types, but they have different names, as shown in the table:

In Flix primitive types are always unboxed. Hence, to call a Java method that expects a java.lang.Integer, if you have a Flix Int32, it must be boxed by calling java.lang.Integer.valueOf.

1. Flix requires at least Java 21. ↩

Creating Objects

In Flix, we can create objects using syntax similar to Java.

For example:

import java.io.File

def main(): Unit \ IO = 
    let f = new File("foo.txt");
    println("Hello World!")

Here we import the java.io.File class and instantiate a File object by calling one of its constructors using the new keyword.

The File class has multiple constructors, so we can also write:

import java.io.File

def main(): Unit \ IO = 
    let f1 = new File("foo.txt");
    let f2 = new File("bar", "foo.txt");
    println("Hello World!")

Flix resolves the constructor based on the number of arguments and their types.

As another example, we can write:

import java.io.File
import java.net.URI

def main(): Unit \ IO = 
    let f1 = new File("foo.txt");
    let f2 = new File("bar", "foo.txt");
    let f3 = new File(new URI("file://foo.txt"));
    println("Hello World!")

We can use a renaming import to resolve a clash between a Java name and a Flix module:

import java.lang.{String => JString}

def main(): Unit \ IO = 
    let s = new JString("Hello World");
    println("Hello World!")

Here JString refers to the Java class java.lang.String whereas String refers to the Flix module. Note that internally Flix and Java strings are the same.

Calling Super Constructors

When creating an anonymous subclass of a Java class, we can define a constructor that calls the parent constructor using super:

import java.lang.Thread

def main(): Unit \ IO =
    let t = new Thread {
        def new(): Thread \ IO = super("my-thread")
        def run(_this: Thread): Unit \ IO =
            println("Hello from ${Thread.currentThread().getName()}")
    };
    t.start()

Here we extend Thread and pass "my-thread" as the thread name to the parent constructor. The constructor is defined with def new() and its body must be exactly a super(...) call. At most one constructor can be defined per new expression.

If no constructor is defined, Flix automatically calls the parent’s no-argument constructor.

Note: Any interaction with Java code always has the IO effect.

Note: In Flix, Java classes must be imported before they can be used. In particular, we cannot write new java.io.File(...).

Calling Object Methods

In Flix, we can call methods on Java objects using syntax similar to Java.

For example:

import java.io.File

def main(): Unit \ IO = 
    let f = new File("foo.txt");
    println(f.getName())

Here we import the java.io.File class, instantiate a File object, and then call the getName method on that object.

Like with constructors, Flix resolves the method based on the number of arguments and their types.

Here is another example:

import java.io.File

def main(): Unit \ IO = 
    let f = new File("foo.txt");
    if (f.exists())
        println("The file ${f.getName()} exists!")
    else
        println("The file ${f.getName()} does not exist!")

And here is a larger example:

import java.io.File
import java.io.FileWriter

def main(): Unit \ IO = 
    let f = new File("foo.txt");
    let w = new FileWriter(f);
    w.append("Hello World\n");
    w.close()

In the above example, we may want to catch the IOException that can be raised:

import java.io.File
import java.io.FileWriter
import java.io.IOException

def main(): Unit \ IO = 
    let f = new File("foo.txt");
    try {
        let w = new FileWriter(f);
        w.append("Hello World\n");
        w.close()
    } catch {
        case ex: IOException => 
            println("Unable to write to file: ${f.getName()}");
            println("The error message was: ${ex.getMessage()}")
    }

Calling Static Methods

In Flix, we can call static methods (i.e. class methods) using syntax similar to Java:

For example:

import java.lang.Math

def main(): Unit \ IO = 
    let n = Math.sin(3.14);
    println(n)

Like with constructors and methods, Flix resolves the static method based on the number of arguments and their types.

Here is another example:

import java.lang.Math

def main(): Unit \ IO = 
    println(Math.abs(-123i32));
    println(Math.abs(-123i64));
    println(Math.abs(-123.456f32));
    println(Math.abs(-123.456f64))

When Constructor or Method Resolution Fails

In some cases the Flix compiler is unable to determine what Java constructor or method is called.

For example, in the program:

import java.lang.{String => JString}

def f(): String \ IO = 
    let o = ???;
    JString.valueOf(o)

The type of o is unknown, hence Flix cannot know if we want to call String.valueOf(boolean), String.valueOf(char), String.valueOf(double), or one of the other overloaded versions.

The solution is to put a type ascription on the relevant argument:

import java.lang.{String => JString}

def f(): String \ IO = 
    let o = ???;
    JString.valueOf((o: Bool))

The type ascription specifies that o has type Bool which allows method resolution to complete successfully. Note that the extra pair of parenthesis is required.

Calling Java Methods Known to be Pure

Any Flix expression that creates a Java object, calls a Java method, or calls a Java static method has the IO effect. This is to be expected: Java constructors and methods may have arbitrary side-effects.

If we know for certain that a Java constructor or method invocation has no side-effects, we can use an unsafe block to tell Flix to treat that expression as pure.

For example:

import java.lang.Math

def pythagoras(x: Float64, y: Float64): Float64 = // Pure, no IO effect
    unsafe Math.sqrt((Math.pow(x, 2.0) + Math.pow(y, 2.0)))

def main(): Unit \ IO = 
    println(pythagoras(3.0, 4.0))

Here we know for certain that Math.pow and Math.sqrt are pure functions, hence we can put them inside an unsafe block. Thus we are able to type check the Flix pythagoras function as pure, i.e. without the IO effect.

Warning: Do not, under any circumstances, use unsafe on expressions that have side-effects. Doing so breaks the type and effect system which can lead to incorrect compiler optimizations which can change the meaning of your program in subtle or catastrophic ways!

Partial Application of Java Constructors and Methods

Flix supports partial application of Flix functions. However, Java constructors and methods can never be partially applied. This limitation can be overcome introducing an explicit lambda.

For example:

import java.lang.{String => JString}

def main(): Unit \ IO = 
    def replaceAll(s, src, dst) = s.replaceAll(src, dst);
    let f = replaceAll("Hello World");
    let s1 = f("World")("Galaxy");
    let s2 = f("World")("Universe");
    println(s1);
    println(s2)

Here we introduce a Flix function replaceAll which calls String.replaceAll. Since replaceAll is a Flix function, we can partially apply it as shown in the example.

Reading and Writing Fields

Flix supports reading object fields and static (class) fields with standard Java syntax.

Reading Object Fields

We can read an object field as follows:

import java.awt.Point

def area(p: Point): Int32 \ IO = p.x * p.y

Reading Static Fields

We can read a static field as follows:

import java.lang.Math

def area(radius: Float64): Float64 = (unsafe Math.PI) * radius * radius

We import the java.lang.Math class and then we access the static PI field.

We know that the PI field will never change, hence we cast away the effect with unsafe.

Classes and Interfaces

Flix allows us to create objects that extend a Java class or implements a Java interface.

This feature is conceptually similar to Java’s Anonymous Classes: We can define an (unnamed class) which implements an interface or extends a class and create an object of that class. All in one expression.

For example, we can create an object that implements the java.lang.Runnable interface:

import java.lang.Runnable

def newRunnable(): Runnable \ IO = new Runnable {
    def $run(_this: Runnable): Unit \ IO = 
        println("I am running!")
}

Every time we call newRunnable we get a fresh object that implements java.lang.Runnable.

Note: The implicit this argument is always explicitly passed as the first argument in a new expression.

As another example, we can create an object that implements the java.io.Closeable interface:

import java.io.Closeable

def newClosable(): Closeable \ IO = new Closeable {
    def close(_this: Closeable): Unit \ IO = 
        println("I am closing!")
}

We can also extend classes. For example, we can create a java.lang.Object where we override the hashCode and toString methods:

def newObject(): Object \ IO = new Object {
    def hashCode(_this: Object): Int32 = 42
    def toString(_this: Object): String = "Hello World!"
}

Calling Super Methods

When overriding a method in an anonymous subclass, we can call the parent class’s implementation using super.methodName(args).

For example, we can extend Thread and override toString to include the parent’s default representation:

import java.lang.Thread

def main(): Unit \ IO =
    let t = new Thread {
        def new(): Thread \ IO = super("my-thread")
        def run(_this: Thread): Unit \ IO =
            println("Hello from ${Thread.currentThread().getName()}")
        def toString(_this: Thread): String \ IO =
            "MyThread(" + super.toString() + ")"
    };
    println(t)

Here super.toString() calls the toString method defined by Thread (the parent class), and we wrap the result in "MyThread(...)".

Note: Super method calls can only be used inside new expressions, i.e. when defining an anonymous subclass.

Nested and Inner Classes

Java supports nested static and non-static inner classes:

For example:

package Foo.Bar;

class OuterClass {
    ...
    class InnerClass {
        ...
    }
    static class StaticInnerClass {
        public static String hello() { return "Hi"; }
    }
}

In Flix, we can access the StaticInnerClass using the import statement:

import Foo.Bar.{OuterClass$StaticInnerClass => Inner}

def main(): Unit \ IO = 
    println(Inner.hello())

A typical example is to access the Map.Entry class:

import java.util.{Map$Entry => Entry}

Note: Flix does not support accessing nested non-static inner classes.

Exceptions

In Flix, we can catch Java exceptions using the try-catch construct. The construct is similar to the one in Java, but the syntax is slightly different.

For example:

import java.io.BufferedReader
import java.io.File
import java.io.FileReader
import java.io.FileNotFoundException
import java.io.IOException

def main(): Unit \ IO = 
    let f = new File("foo.txt");
    try {
        let r = new BufferedReader(new FileReader(f));
        let l = r.readLine();
        println("The first line of the file is: ${l}");
        r.close()
    } catch {
        case _: FileNotFoundException => 
            println("The file does not exist!")
        case ex: IOException => 
            println("The file could not be read!");
            println("The error message was: ${ex.getMessage()}")
    }

Here the calls new FileReader(), r.readLine(), and r.close() can throw IOExceptions. We use a try-catch block to catch these exceptions. We add a special case for the FileNotFoundException exception.

Note: Flix programs should not use exceptions: it is considered bad style. Instead, programs should use the Result[e, t] type. The try-catch construct should only be used on the boundary between Flix and Java code.

Note: Flix does not (yet) support a finally block.

Boxing and Unboxing

Unlike Java, Flix never performs implicit boxing or unboxing of values.

We believe auto boxing is a design flaw and do not plan to support it. Hence, primitive values must be manually boxed and unboxed.

Boxing

The following example shows how to box a primitive integer:

def f(x: Int32): String \ IO = 
    let i = Box.box(x); // Integer
    i.toString()

Here the call to Box.box(x) returns an Integer object. Since i is an object, we can call toString on it. Boxing is a pure operation, but calling toString has the IO effect.

Unboxing

The following example shows how to unbox two Java Integer objects:

import java.lang.Integer

def sum(x: Integer, y: Integer): Int32 = 
    Box.unbox(x) + Box.unbox(y)

Here the call to Box.unbox returns an Int32 primitive value.

Unboxing is a pure operation.

Java Collections

Flix has support for conversion from and to Java collections.

In the following, we use the following import aliases:

import java.util.{List => JList}
import java.util.{LinkedList => JLinkedList}
import java.util.{ArrayList => JArrayList}
import java.util.{Set => JSet}
import java.util.{TreeSet => JTreeSet}
import java.util.{Map => JMap}
import java.util.{TreeMap => JTreeMap}

The following functions are available in the Adaptor module:

Flix to Java

The following functions convert Flix collections to Java collections:

///
/// Lists
///
def toList(ma: m[a]): JList[a] \ IO + Aef[m] with Foldable[m]
def toArrayList(ma: m[a]): JArrayList[a] \ IO + Aef[m] with Foldable[m]
def toLinkedList(ma: m[a]): JLinkedList[a] \ IO + Aef[m] with Foldable[m]

///
/// Sets
///
def toSet(ma: m[a]): JSet[a] \ IO + Aef[m] with Order[a], Foldable[m]
def toTreeSet(ma: m[a]): JTreeSet[a] \ IO + Aef[m] with Order[a], Foldable[m]

///
/// Maps
///
def toMap(m: Map[k, v]): JMap[k, v] \ IO with Order[k]
def toTreeMap(m: Map[k, v]): JTreeMap[k, v] \ IO with Order[k]

Each function constructs a new collection and copies all its elements into it. Hence each operation takes at least linear time. The result is a normal Java collection (which can be modified).

Java to Flix

The following functions convert Java collections to Flix collections:

/// Lists
def fromList(l: JList[a]): List[a]

/// Sets
def fromSet(l: JSet[a]): Set[a] with Order[a]

/// Maps
def fromMap(m: JMap[k, v]): Map[k, v] with Order[k]

Each function constructs a new Flix collection from a Java Collection. Hence each operation takes at least linear time. Note that for Set and Map, the Flix collections use the Order[a] instance defined on a. This may not be the same ordering as used by Java.

Warning: Converting Flix and/or Java collections with primitive values requires extra care. In particular, values must be manually boxed or unboxed before any conversion.

Fixpoints

A unique feature of Flix is its built-in support for fixpoint computations on constraint on relations and constraint on lattices.

We assume that the reader is already familiar with Datalog and focus on the Flix specific features.

Using Flix to Solve Constraints on Relations

We can use Flix to solve a fixpoint computation inside a function.

For example, given a set of edges s, a src node, and dst node, compute if there is a path from src to dst. We can elegantly solve this problem as follows:

def isConnected(s: Set[(Int32, Int32)], src: Int32, dst: Int32): Bool =
    let rules = #{
        Path(x, y) :- Edge(x, y).
        Path(x, z) :- Path(x, y), Edge(y, z).
    };
    let edges = inject s into Edge/2;
    let paths = query edges, rules select true from Path(src, dst);
    not (paths |> Vector.isEmpty)

def main(): Unit \ IO =
    let s = Set#{(1, 2), (2, 3), (3, 4), (4, 5)};
    let src = 1;
    let dst = 5;
    if (isConnected(s, src, dst)) {
        println("Found a path between ${src} and ${dst}!")
    } else {
        println("Did not find a path between ${src} and ${dst}!")
    }

The isConnected function behaves like any other function: We can call it with a set of edges (Int32-pairs), an Int32 source node, and an Int32 destination node. What is interesting about isConnected is that its implementation uses a small Datalog program to solve the task at hand.

In the isConnected function, the local variable rules holds a Datalog program fragment that consists of two rules which define the Path relation. Note that the predicate symbols, Edge and Path do not have to be explicitly introduced; they are simply used. The local variable edges holds a collection of edge facts that are obtained by taking all the tuples in the set s and turning them into Edge facts. Next, the local variable paths holds the result of computing the fixpoint of the facts and rules (edges and rules) and selecting the Boolean true if there is a Path(src, dst) fact. Note that here src and dst are the lexically-bound function parameters. Thus, paths is either an empty array (no paths were found) or a one-element array (a path was found), and we simply return this fact.

Flix is strongly typed. Any attempt to use predicate symbol with terms of the wrong type (or with the wrong arity) is caught by the type checker. Note also that Flix supports type inference, hence we did not have to declare the type of Edge nor of Path.

Programming with First-class Constraints

A unique feature of Flix is its support for first-class constraints. A first-class constraint is a value that can be constructed, passed around, composed with other constraints, and ultimately solved. The solution to a constraint system is another constraint system which can be further composed. For example:

def getParents(): #{ ParentOf(String, String) | r } = #{
    ParentOf("Pompey", "Strabo").
    ParentOf("Gnaeus", "Pompey").
    ParentOf("Pompeia", "Pompey").
    ParentOf("Sextus", "Pompey").
}

def getAdoptions(): #{ AdoptedBy(String, String) | r } = #{
    AdoptedBy("Augustus", "Caesar").
    AdoptedBy("Tiberius", "Augustus").
}

def withAncestors(): #{ ParentOf(String, String),
                        AncestorOf(String, String) | r } = #{
        AncestorOf(x, y) :- ParentOf(x, y).
        AncestorOf(x, z) :- AncestorOf(x, y), AncestorOf(y, z).
}

def withAdoptions(): #{ AdoptedBy(String, String),
                        AncestorOf(String, String) | r } = #{
    AncestorOf(x, y) :- AdoptedBy(x, y).
}

def main(): Unit \ IO =
    let c = false;
    if (c) {
        query getParents(), getAdoptions(), withAncestors()
            select (x, y) from AncestorOf(x, y) |> println
    } else {
        query getParents(), getAdoptions(), withAncestors(), withAdoptions()
            select (x, y) from AncestorOf(x, y) |> println
    }

The program uses three predicate symbols: ParentOf, AncestorOf, and AdoptedBy. The getParentsfunction returns a collection of facts that represent biological parents, whereas the getAdoptions function returns a collection of facts that represent adoptions. The withAncestors function returns two constraints that populate the AncestorOf relation using the ParentOf relation. The withAdoptions function returns a constraint that populates the ParentOf relation using the AdoptedBy relation.

In the main function the local variable c controls whether we query a Datalog program that only considers biological parents or if we include adoptions.

As can be seen, the types the functions are row-polymorphic. For example, the signature of getParents is def getParents(): #{ ParentOf | r } where r is row polymorphic type variable that represent the rest of the predicates that the result of the function can be composed with.

Design Note

The row polymorphic types are best understood as an over-approximation of the predicates that may occur in a constraint system. For example, if a constraint system has type #{ A(String), B(Int32, Int32) } that doesn’t necessarily mean that it will contain facts or rules that use the predicate symbols A or B, but it does guarantee that it will not contain any fact or rule that refer to a predicate symbol C.

Polymorphic First-class Constraints

Another unique feature of Flix is its support for first-class polymorphic constraints. That is, constraints where one or more constraints are polymorphic in their term types. For example:

def edgesWithNumbers(): #{ LabelledEdge(String, Int32 , String) | r } = #{
    LabelledEdge("a", 1, "b").
    LabelledEdge("b", 1, "c").
    LabelledEdge("c", 2, "d").
}

def edgesWithColor(): #{ LabelledEdge(String, String, String) | r } = #{
    LabelledEdge("a", "red", "b").
    LabelledEdge("b", "red", "c").
    LabelledEdge("c", "blu", "d").
}

def closure(): #{ LabelledEdge(String, l, String),
                  LabelledPath(String, l, String) } with Order[l] = #{
    LabelledPath(x, l, y) :- LabelledEdge(x, l, y).
    LabelledPath(x, l, z) :- LabelledPath(x, l, y), LabelledPath(y, l, z).
}

def main(): Unit \ IO =
    query edgesWithNumbers(), closure()
        select (x, l, z) from LabelledPath(x, l, z) |> println;
    query edgesWithColor(), closure()
        select (x, l, z) from LabelledPath(x, l, z) |> println

Here we use two predicate symbols: LabelledEdge and LabelledPath. Each predicate has a type parameter named l and is polymorphic in the “label” type associated with the edge/path. Note how edgesWithNumbers returns a collection of edge facts where the labels are integers, whereas edgesWithColor returns a collection of facts where the labels are strings. The closure function is polymorphic and returns two rules that compute the transitive closure of edges that have the same label.

The Flix type system ensures that we cannot accidentally mix edges (or paths) with different types of labels.

Injecting Facts into Datalog

Flix provides a flexible mechanism that allows functional data structures (such as lists, sets, and maps) to be converted into Datalog facts.

For example, given a Flix list of pairs we can convert it to a collection of Datalog facts:

let l = (1, 2) :: (2, 3) :: Nil;
let p = inject l into Edge/2;

where l has type List[(Int32, Int32)]. The inject expression converts l into a Datalog constraint set p of type #{ Edge(Int32, Int32) | ... }. The expression includes the predicate’s arity: Edge/2. The general form is Predicate/Arity.

The inject expression works with any type that implements the Foldable trait. Consequently, it can be used with lists, sets, maps, and so forth.

The inject expression can operate on multiple collections simultaneously. For example:

let names = "Lucky Luke" :: "Luke Skywalker" :: Nil;
let jedis = "Luke Skywalker" :: Nil;
let p = inject names, jedis into Name/1, Jedi/1;

where p has type #{ Name(String), Jedi(String) | ... }.

Pipelines of Fixpoint Computations

The solution (i.e. fixpoint) of a constraint system is another constraint system. We can use this to construct pipelines of fixpoint computations, i.e. to feed the result of one fixpoint computation into another fixpoint computation. For example:

def main(): Unit \ IO =
    let f1 = #{
        ColorEdge(1, "blue", 2).
        ColorEdge(2, "blue", 3).
        ColorEdge(3, "red", 4).
    };
    let r1 = #{
        ColorPath(x, c, y) :- ColorEdge(x, c, y).
        ColorPath(x, c, z) :- ColorPath(x, c, y), ColorEdge(y, c, z).
    };
    let r2 = #{
        ColorlessPath(x, y) :- ColorPath(x, _, y).
    };
    let m = solve f1, r1 project ColorPath;
    query m, r2 select (x, y) from ColorlessPath(x, y) |> println

The program uses three predicates: ColorEdge, ColorPath, and ColorlessPath. Our goal is to compute the transitive closure of the colored edges and then afterwards construct a graph where the edges have no color.

The program first computes the fixpoint of f1 and r1 and injects out the ColorPath fact. The result is stored in m. Next, the program queries m and r2, and selects all ColorlessPath facts.

Stratified Negation

Flix supports stratified negation which allow restricted use of negation in rule bodies. For example:

def main(): Unit \ IO =
    let movies = #{
        Movie("The Hateful Eight").
        Movie("Interstellar").
    };
    let actors = #{
        StarringIn("The Hateful Eight", "Samuel L. Jackson").
        StarringIn("The Hateful Eight", "Kurt Russel").
        StarringIn("The Hateful Eight", "Quentin Tarantino").
        StarringIn("Interstellar", "Matthew McConaughey").
        StarringIn("Interstellar", "Anne Hathaway").
    };
    let directors = #{
        DirectedBy("The Hateful Eight", "Quentin Tarantino").
        DirectedBy("Interstellar", "Christopher Nolan").
    };
    let rule = #{
        MovieWithoutDirector(title) :-
            Movie(title),
            DirectedBy(title, name),
            not StarringIn(title, name).
    };
    query movies, actors, directors, rule
        select title from MovieWithoutDirector(title) |> println

The program defines three local variables that contain information about movies, actors, and directors. The local variable rule contains a rule that captures all movies where the director does not star in the movie. Note the use negation in this rule. The query returns an array with the string "Interstellar" because Christopher Nolan did not star in that movie.

Note: Flix enforces that programs are stratified, i.e. a program must not have recursive dependencies on which there is use of negation. If there is, the Flix compiler rejects the program.

Local Predicates

Flix supports an abstract mechanism called local predicates. A local predicate, like a local variable, is not visible to the outside.

To understand local predicates, consider the following example: We can a write a function that returns a Datalog program value which computes whether a graph has a cycle:

def cyclic(): #{Edge(Int32, Int32), Path(Int32, Int32), Cyclic()} = #{
    Path(x, y) :- Edge(x, y).
    Path(x, z) :- Path(x, y), Edge(y, z).
    Cyclic() :- Path(x, x).
}

def main(): Unit \ IO = 
    let db = #{
        Edge(1, 2).
        Edge(2, 3).
        Edge(3, 1).
    };
    query db, cyclic() select true from Cyclic() |> println

Here the cyclic function returns a Datalog program value which consists of three rules that compute the transitive closure of a graph of edges and whether there is path from a vertex to itself. We use the cyclic function inside main to determine if a small graph, given by db, has a cyclic. The program prints Vector#{true} when compiled and run.

Returning to cyclic, we see that its type is:

def cyclic(): #{Edge(Int32, Int32), Path(Int32, Int32), Cyclic()} = ...

This is sensible because the Datalog program value uses the predicate symbols Edge, Path and Cyclic with their given types. However, if we think more about it, we can realize that the Path predicate is really local to the computation: We are not meant to see it from the outside; it is an implementation detail! What we really want is that Edge(Int32, Int32) should be an input and Cyclic() should be an output. More importantly, Path(Int32, Int32) should not be visible from the outside nor part of the type. We can achieve this with predicate abstraction:

def cyclic(): #{Edge(Int32, Int32), Cyclic()} = 
    #(Edge, Cyclic) -> #{
        Path(x, y) :- Edge(x, y).
        Path(x, z) :- Path(x, y), Edge(y, z).
        Cyclic() :- Path(x, x).
    }

Here we use the syntax #(Edge, Cyclic) -> v to specific that only the predicates Edge and Cyclic from within v should be visible to the outside. Thus we can omit Path(Int32, Int32) from the return type of cyclic. Moreover, the Datalog program value no longer contains a Path predicate symbol that can be referenced. We can evidence this by observing that the program:

def main(): Unit \ IO = 
    let db = #{
        Edge(1, 2).
        Edge(2, 3).
        Edge(3, 1).
    };
    query db, cyclic() select (x, y) from Path(x, y) |> println

prints the empty vector Vector#{} since Path has been made local by the predicate abstraction.

Functional Predicates

We sometimes run into a situation where we would like to use a logic predicate, but not to exhaustively enumerate all of its tuples.

For example, we can image a situation where we want a predicate PrimeInRange(from, to, prime) which holds if prime is a prime number in the range [from; to]. While we can imagine such a predicate, it is not feasible to compute with. Instead, what we often want, is that we want to treat PrimeInRange as a functional, i.e. a function that given from and to as input produces a set of primes as output. To make matters concrete, we might want to write the rule:

R(p) :- P(x), Q(y), PrimeInRange(x, y, p).

but without having to evaluate PrimeInRange for every x, y, and p.

We can achieve this as follows. We write a function:

def primesInRange(b: Int32, e: Int32): Vector[Int32] = 
    Vector.range(b, e) |> Vector.filter(isPrime)

The key is that primesInRange is a function which returns a vector of tuples (in this case single elements), given a begin b and end index e. Thus primesInRange can efficiently compute the tuples we are interested in. To use it in our rule, we write:

R(p) :- P(b), Q(e), let p = primesInRange(b, e).

where b and e are clearly identified as the input of primesInRange and p as its output. Specifically, Flix requires that b and e are positively bound (i.e. bound by a non-negative body atom– in this case P and Q.) In this case, primesInRanges returns a vector of Int32s, but in general a functional may return a vector of tuples.

Note: An important limitation in the current implementation is that the variables in the LHS of a functional predicate must not be rebound. That is, if the functional predicate is of the form let (a, b) = f(x, y) then a and b must not be rebound in the rule.

Using Flix to Solve Constraints on Lattices

Flix supports not only constraints on relations, but also constraints on lattices. To create such constraints, we must first define the lattice operations (the partial order, the least upper bound, and so on) as functions, associate them with a type, and then declare the predicate symbols that have lattice semantics.

We begin with the definition of the Sign data type:

use Sign.{Top, Neg, Zer, Pos, Bot};

enum Sign {
    case Top,
    case Neg,
    case Zer,
    case Pos,
    case Bot
}

We need to define the usual Eq, Order, and ToString instances for this new type. Note that the order instance is unrelated to the partial order instance we will later define, and is simply used to sort elements for pretty printing etc.

instance Eq[Sign] {
    pub def eq(x: Sign, y: Sign): Bool = match (x, y) {
        case (Bot, Bot) => true
        case (Neg, Neg) => true
        case (Zer, Zer) => true
        case (Pos, Pos) => true
        case (Top, Top) => true
        case _          => false
    }
}

instance Order[Sign] {
    pub def compare(x: Sign, y: Sign): Comparison =
        let num = w -> match w {
            case Bot => 0
            case Neg => 1
            case Zer => 2
            case Pos => 3
            case Top => 4
        };
        num(x) <=> num(y)
}

instance ToString[Sign] {
    pub def toString(x: Sign): String = match x {
        case Bot => "Bot"
        case Neg => "Neg"
        case Zer => "Zer"
        case Pos => "Pos"
        case Top => "Top"
    }
}

With these trait instances in place, we can now define the lattice operations on Sign.

We define the bottom element and the partial order:

instance LowerBound[Sign] {
    pub def minValue(): Sign = Bot
}

instance PartialOrder[Sign] {
    pub def lessEqual(x: Sign, y: Sign): Bool =
        match (x, y) {
            case (Bot, _)   => true
            case (Neg, Neg) => true
            case (Zer, Zer) => true
            case (Pos, Pos) => true
            case (_, Top)   => true
            case _          => false
        }
}

Next, we define the least upper bound and greatest lower bound:

instance JoinLattice[Sign] {
    pub def leastUpperBound(x: Sign, y: Sign): Sign =
        match (x, y) {
            case (Bot, _)   => y
            case (_, Bot)   => x
            case (Neg, Neg) => Neg
            case (Zer, Zer) => Zer
            case (Pos, Pos) => Pos
            case _          => Top
        }
}

instance MeetLattice[Sign] {
    pub def greatestLowerBound(x: Sign, y: Sign): Sign =
        match (x, y) {
            case (Top, _)   => y
            case (_, Top)   => x
            case (Neg, Neg) => Neg
            case (Zer, Zer) => Zer
            case (Pos, Pos) => Pos
            case _          => Bot
        }
}

With all of these definitions we are ready to write Datalog constraints with lattice semantics. But before we proceed, let us also write a single monotone function:

def sum(x: Sign, y: Sign): Sign = match (x, y) {
    case (Bot, _)   => Bot
    case (_, Bot)   => Bot
    case (Neg, Zer) => Neg
    case (Zer, Neg) => Neg
    case (Zer, Zer) => Zer
    case (Zer, Pos) => Pos
    case (Pos, Zer) => Pos
    case (Pos, Pos) => Pos
    case _          => Top
}

We can now finally put everything to use:

pub def main(): Unit \ IO =
    let p = #{
        LocalVar("x"; Pos).
        LocalVar("y"; Zer).
        LocalVar("z"; Neg).
        AddStm("r1", "x", "y").
        AddStm("r2", "x", "y").
        AddStm("r2", "y", "z").
        LocalVar(r; sum(v1, v2)) :-
            AddStm(r, x, y), LocalVar(x; v1), LocalVar(y; v2).
    };
    query p select (r, v) from LocalVar(r; v) |> println

Note the careful use of ; to designate lattice semantics.

Using Lattice Semantics to Compute Shortest Paths

We can also use lattice semantics to compute shortest paths.

The key is to define our own new data type D which is simple an Int32 with forms a lattice with the reverse order of the integers (e.g. the smallest element is Int32.maxValue()).

use D.D;

pub enum D with Eq, Order, ToString {
    case D(Int32)
}

instance PartialOrder[D] {
    pub def lessEqual(x: D, y: D): Bool =
        let D(n1) = x;
        let D(n2) = y;
        n1 >= n2        // Note: Order reversed.
}

instance LowerBound[D] {
    // Note: Because the order is reversed, the largest value is the smallest.
    pub def minValue(): D = D(Int32.maxValue())
}

instance UpperBound[D] {
    // Note: Because the order is reversed, the smallest value is the largest.
    pub def maxValue(): D = D(Int32.minValue())
}

instance JoinLattice[D] {
    pub def leastUpperBound(x: D, y: D): D =
        let D(n1) = x;
        let D(n2) = y;
        D(Int32.min(n1, n2))        // Note: Order reversed.
}

instance MeetLattice[D] {
    pub def greatestLowerBound(x: D, y: D): D =
        let D(n1) = x;
        let D(n2) = y;
        D(Int32.max(n1, n2))        // Note: Order reversed.
}

def shortestPath(g: Set[(t, Int32, t)], o: t): Map[t, D] with Order[t] =
    let db = inject g into Edge/3;
    let pr = #{
        Dist(o; D(0)).
        Dist(y; add(d1 , D(d2))) :- Dist(x; d1), Edge(x, d2, y).
    };
    query db, pr select (x , d) from Dist(x; d) |> Vector.toMap

def add(x: D, y: D): D =
    let D(n1) = x;
    let D(n2) = y;
    D(n1 + n2)

def main(): Unit \ IO =
    let g = Set#{
        ("Aarhus", 200, "Flensburg"),
        ("Flensburg", 150, "Hamburg")
    };
    println(shortestPath(g, "Aarhus"))

Flix actually comes with a type like D built-in. It’s called Down and simply reverses the order on the underlying type. We can use it and write the program as:

use Down.Down;

def shortestPaths(g: Set[(t, Int32, t)], o: t): Map[t, Down[Int32]] with Order[t] =
    let db = inject g into Edge/3;
    let pr = #{
        Dist(o; Down(0)).
        Dist(y; add(d1 , Down(d2))) :- Dist(x; d1), Edge(x, d2, y).
    };
    query db, pr select (x , d) from Dist(x; d) |> Vector.toMap

def add(x: Down[Int32], y: Down[Int32]): Down[Int32] =
    let Down(n1) = x;
    let Down(n2) = y;
    Down(n1 + n2)

def main(): Unit \ IO =
    let g = Set#{
        ("Aarhus", 200, "Flensburg"),
        ("Flensburg", 150, "Hamburg")
    };
    println(shortestPaths(g, "Aarhus"))

Everyday Programming

In this chapter we cover some everyday programming features:

• The signature of the main function.
• How to print to standard out and standard error.
• How to use string interpolation.
• How to use anonymous and named holes for incomplete programs.
• How to use type ascriptions to explicitly provide some types to the compiler.

The Main Function

The entry point of any Flix program is the main function which must take zero arguments and return Unit:

def main(): Unit \ IO =
    println("Hello World!")

Effects of Main

The main function can use any combination of:

• Primitive effects: IO and NonDet.
• Any effect with a default handler: for example Env, Exit, Clock, Logger, and others.

Effects with default handlers are automatically translated into IO by the Flix compiler. See Default Handlers for details.

For example, main can use the Env and Exit effects:

use Sys.Env
use Sys.Exit

def main(): Unit \ {Env, Exit} =
    let args = Env.getArgs();
    match List.head(args) {
        case None    =>
            println("Missing argument.");
            Exit.exit(1)
        case Some(a) =>
            println("Hello ${a}!")
    }

Accessing Command Line Arguments

The command line arguments passed to the program can be accessed by calling Env.getArgs() through the Env effect:

use Sys.Env

def main(): Unit \ {Env, IO} =
    let args = Env.getArgs();
    println("Arguments: ${args}")

Exiting the Program

The program can be terminated with a specific exit code using Exit.exit:

use Sys.Exit

def main(): Unit \ Exit =
    Exit.exit(0)

Why Must Main Be Effectful?

Flix requires main to be effectful. If main was pure there would be no reason to run the program. Typically this requirement is satisfied because main prints to the console or has another side-effect.

Printing to Standard Out

The Flix Prelude defines the println function which prints to standard out. For example:

println("Hello World")

The println function can print any value whose type implements the ToString trait and consequently can be converted to a String. For example:

let o = Some(123);
let l = 1 :: 2 :: 3 :: Nil;
println(o);
println(l)

The println function is rightfully effectful, hence it cannot be called from a pure function. To debug a pure function, use the builtin debugging facilities.

The Console Effect

The Console effect defines operations for reading from and writing to the terminal:

eff Console {
    def readln(): String
    def print(s: String): Unit
    def eprint(s: String): Unit
    def println(s: String): Unit
    def eprintln(s: String): Unit
}

String Interpolation

Flix strings support interpolation. Inside a string, the form "${e}" evaluates e to a value and converts it to a string using the ToString trait. For example:

let fstName = "Lucky";
let lstName = "Luke";
"Hello Mr. ${lstName}. Do you feel ${fstName}, punk?"

String interpolation works for any type that implements a ToString instance. For example:

let i = 123;
let o = Some(123);
let l = 1 :: 2 :: 3 :: Nil;
"i = ${i}, o = ${o}, l = ${l}"

String interpolations may contain arbitrary expressions. For example:

let x = 1;
let y = 2;
"${x + y + 1}"

String interpolation is the preferred way to concatenate two strings:

let x = "Hello";
let y = "World";
"${x}${y}" // equivalent to x + y

String interpolation is the preferred way to convert a value to a string:

let o = Some(123);
"${o}"

which is equivalent to an explicit use of the toString function from the ToString trait:

ToString.toString(o)

String interpolators may nest, but this is discouraged.

Tail Recursion

In Flix, and in functional programming in general, iteration is expressed through recursion.

For example, if we want to determine if a list contains an element, we can write a recursive function:

def memberOf(x: a, l: List[a]): Bool with Eq[a] = 
    match l {
        case Nil     => false
        case y :: ys => if (x == y) true else memberOf(x, ys)
    }

The memberOf function pattern matches on the list l. If it is empty then it returns false. Otherwise, we have an element y and the rest of the list is ys. If x == y then we have found the element and we return true. Otherwise we recurse on the rest of the list ys.

The recursive call to memberOf is in tail position, i.e. it is the last thing to happen in the memberOf function. This has two important benefits: (a) the Flix compiler is able to rewrite memberOf to use an ordinary loop (which is more efficient than a function call) and more importantly (b) a call to memberOf cannot overflow the stack, because the call stack never increases in height.

Tip: Flix has support for full tail call elimination which means that recursive calls in tail position never increase the stack height and hence cannot cause the stack to overflow!

We remark that Flix has full tail call elimination, not just tail call optimization. This means that the following program compiles and runs successfully:

def isOdd(n: Int32): Bool =
    if (n == 0) false else isEvn(n - 1)

def isEvn(n: Int32): Bool =
    if (n == 0) true else isOdd(n - 1)

def main(): Unit \ IO =
    isOdd(12345) |> println

which is not the case in many other programming languages.

Non-Tail Calls and StackOverflows

While the Flix compiler guarantees that tail calls cannot overflow the stack, the same is not true for function calls in non-tail positions.

For example, the following implementation of the factorial function overflows the call stack:

def factorial(n: Int32): Int32 = match n {
    case 0 => 1
    case _ => n * factorial(n - 1)
}

as this program shows:

def main(): Unit \ IO = 
    println(factorial(1_000_000))

which when compiled and run produces:

java : Exception in thread "main" java.lang.StackOverflowError
	at Cont%Int32.unwind(Cont%Int32)
	at Def%factorial.invoke(Unknown Source)
	at Cont%Int32.unwind(Cont%Int32)
	at Def%factorial.invoke(Unknown Source)
	at Cont%Int32.unwind(Cont%Int32)
    ... many more frames ...

A well-known technique is to rewrite factorial to use an accumulator:

def factorial(n: Int32): Int32 = 
    def visit(x, acc) = match x {
        case 0 => acc
        case _ => visit(x - 1, x * acc)
    };
    visit(n, 1)

Here the visit function is tail recursive, hence it cannot overflow the stack.

The @Tailrec Annotation

Flix provides the @Tailrec annotation, which asks the compiler to verify that every self-recursive call in a function is in tail position. The annotation is optional and does not change runtime behavior — it serves as a documentation and verification tool.

For example, an accumulator-style sum function is tail recursive:

@Tailrec
def sum(l: List[Int32], acc: Int32): Int32 = match l {
    case Nil     => acc
    case x :: xs => sum(xs, acc + x)
}

The compiler accepts this because the recursive call to sum is the last operation in the function — nothing further is done with its result.

In contrast, the following function is rejected:

@Tailrec
def length(l: List[Int32]): Int32 = match l {
    case Nil     => 0
    case _ :: xs => length(xs) + 1
}

Here, the result of length(xs) is used in an addition (+ 1), so the recursive call is not in tail position. The compiler reports an error:

>> Non-tail recursive call in @Tailrec function 'length'.

   ... length(xs) + 1
       ^^^^^^^^^^
       non-tail recursive call

To fix this, rewrite the function to use an accumulator, as shown above.

Tip: The @Tailrec annotation is purely a compile-time check. It does not affect code generation — Flix already performs full tail call elimination for any call in tail position, whether annotated or not. Use @Tailrec when you want the compiler to guarantee that a function remains tail recursive as the code evolves.

Anonymous and Named Holes

During development, Flix encourages the use of holes for incomplete code. For example:

def sum(x: Int32, y: Int32): Int32 = ???

The triple question marks ??? represents an anonymous hole and can be used wherever an expression is expected. In the above code, ??? represents a missing function body, but it can also be used inside an expression. For example:

def length(l: List[a]): Int32 = match l {
    case Nil     => 0
    case x :: xs => ???
}

When a program has multiple holes, it can be useful to name them. For example:

def length(l: List[a]): Int32 = match l {
    case Nil     => ?base
    case x :: xs => ?step
}

Flix requires that each named hole has a unique name.

Variable Holes and Auto-Completion

Flix has support for a special variable hole which enables type-driven auto-completion suggestions. For example, in the program:

def main(): Unit \ IO = 
    let s: String = "Hello World";
    let n: Int32 = s?;
    println("The length of ${s} is ${n}!")

If we place the cursor on s? and ask for auto-completion suggestions, Flix will suggest:

• String.length(s: String): Int32
• String.countSubstring(substr: {substr: String}, s: String): Int32
• String.levenshtein(s: String, t: String): Int32
• …

since these are functions that can convert a String to an Int32.

As another example, in the program:

def main(): Unit \ IO = 
    let l: List[Int32] = List.range(1, 10);
    let n: Int32 = l?;
    println("The value of `n` is ${n}.")

If we place the cursor on l?, Flix will suggest:

• List.product(l: List[Int32]): Int32
• List.sum(l: List[Int32]): Int32
• List.fold(l: List[Int32]): Int32
• List.length(l: List[Int32]): Int32
• List.count(f: a -> Bool \ ef, l: List[a]): a \ ef
• …

since these are functions that can convert a List[Int32] to an Int32.

Type Ascriptions

While Flix supports local type inference, it can sometimes be useful to annotate an expression or a let-binding with its type. We call such annotations type ascriptions. A type ascription cannot change the type of an expression nor can it be used to violate type safety.

A type ascription can be placed after an expression:

(("Hello" :: "World" :: Nil) : List[String])

but it must be wrapped in parentheses to disambiguate it from other expressions.

It can also be placed on a let-binding without parentheses:

let l: List[String] = "Hello" :: "World" :: Nil

Kind Ascriptions

Flix also supports kind ascriptions. Where a type ascription specifies the type of an expression, a kind ascription specifies the kind of a type.

We can use kind ascriptions on type parameters. For example:

def fst1[a: Type, b: Type](p: (a, b)): a = let (x, _) = p; x

Here we have specified that the kind of the two type parameters a and b is Type. We will typically never have to specify such kinds since they can be inferred.

We can also provide kind ascriptions on algebraic data types:

enum A[t: Type] {
    case A(t, t)
}

and on traits:

trait MyTrait[t: Type] {
    // ...
}

We typically only use kind ascriptions for higher-kinded types.

Redundancy

The Flix compiler aggressively rejects programs that contain unused elements. The idea is to help programmers avoid subtle bugs[^1]. While this can take some time getting used to, we believe the trade-off is worth it.

Specifically, the Flix compiler will ensure that a program does not have:

• Unused local variables: local variables that are declared, but never used.
• Shadowed local variables: local variables that shadow other local variables.
• Useless expressions: pure expressions whose values are discarded.
• Must use values: expressions whose values are unused but their type is marked as @MustUse.

Unused Local Variables

Flix rejects programs with unused variables.

For example, the following program is rejected:

def main(): Unit \ IO =
    let x = 123;
    let y = 456;
    println("The sum is ${x + x}")

with the message:

❌ -- Redundancy Error -------------------------------------------------- Main.flix

>> Unused local variable 'y'. The variable is not referenced within its scope.

3 |     let y = 456;
            ^
            unused local variable.

Unused local variables can be prefixed by an underscore _ to suppress the error. For example, if we replace y by _y the above program compiles:

def main(): Unit \ IO =
    let x = 123;
    let _y = 456; // OK
    println("The sum is ${x + x}")

Shadowed Local Variables

Flix rejects programs with shadowed variables.

For example, the following program is rejected:

def main(): Unit \ IO =
    let x = 123;
    let x = 456;
    println("The value of x is ${x}.")

with the message:

❌ -- Redundancy Error -------------------------------------------------- Main.flix

>> Shadowed variable 'x'.

3 |     let x = 456;
            ^
            shadowing variable.

The shadowed variable was declared here:

2 |     let x = 123;
            ^
            shadowed variable.

Useless Expressions

Flix rejects programs with pure expressions whose results are discarded.

For example, the following program is rejected:

def main(): Unit \ IO =
    123 + 456;
    println("Hello World!")

with the message:

❌ -- Redundancy Error -------------------------------------------------- Main.flix

>> Useless expression: It has no side-effect(s) and its result is discarded.

2 |     123 + 456;
        ^^^^^^^^^
        useless expression.

The expression has type 'Int32'

An expression that has no side-effect and whose result is unused is suspicious, since it could just be removed from the program without changing its meaning.

Must Use Values

Flix rejects programs with expressions whose values are discarded but where their type is marked with the @MustUse annotation. Function types, and the Result and Validation types from the Flix Standard Library are marked as @MustUse.

For example, the following program is rejected:

def main(): Unit \ IO =
    File.creationTime("foo.txt");
    println("Hello World!")

with the message:

❌ -- Redundancy Error -------------------------------------------------- Main.flix

>> Unused value but its type is marked as @MustUse.

2 |     File.creationTime("foo.txt");
        ^^^^^^^^^^^^^^^^^^^^^^^^^^^^
        unused value.

The expression has type 'Result[String, Int64]'

Even though File.creationTime has a side-effect, we should probably be using the result Result[String, Int64]. At least to ensure that the operation was successful.

If the result of an impure expression is truly not needed, then the discard expression can be used:

def main(): Unit \ IO =
    discard File.creationTime("foo.txt");
    println("Hello World!")

which permits a @MustUse value to be thrown away as long as the expression is non-pure.

[^1] See e.g. Using Redundancies to Find Errors.

Debugging

When debugging, it is often helpful to output the value of an expression or variable.

We might try something like:

def sum(x: Int32, y: Int32): Int32 =
    let result = x + y;
    println("The sum of ${x} and ${y} is ${result}");
    result

Unfortunately this does not work:

❌ -- Type Error -------------------------------------------------- Main.flix

>> Unable to unify the effect formulas: 'IO' and 'Pure'.

1 |> def sum(x: Int32, y: Int32): Int32 =
2 |>     let result = x + y;
3 |>     println("The sum of ${x} and ${y} is ${result}");
4 |>     result

The problem is that println has the IO. Hence, we cannot use it to for print debugging inside pure functions. We could make our sum function have the IO effect, but that is rarely what we want. Instead, Flix has a built-in debugging facility that allows us to do print-line debugging.

The Debug.dprintln Function

Instead, we can use the Debug.dprintln function and write:

use Debug.dprintln;

def sum(x: Int32, y: Int32): Int32 =
    let result = x + y;
    dprintln("The sum of ${x} and ${y} is ${result}");
    result

Inside the sum function, the dprintln has the effect Debug, but due to its special nature, the Debug effect “disappears” once we exit the function, i.e. it is not part of its type and effect signature.

Debugging with Source Locations

We can use the special debug string interpolator to add source locations to our print statements:

use Debug.dprintln;

def sum(x: Int32, y: Int32): Int32 =
    let result = x + y;
    dprintln(d"The sum of ${x} and ${y} is ${result}");
    result

A longer introduction to dprintln is available in the blog post Effect Systems vs Print Debugging: A Pragmatic Solution

Tools

This chapter covers the tooling which Flix ships with, including:

• A fully-featured Visual Studio Code extension.
• A built-in test framework.

Visual Studio Code Extension

Flix comes with a fully-featured Visual Studio Code Extension:

The Flix extension uses the real Flix compiler hence all information (e.g. error messages) are always 1:1 with the real Flix programming language.

Flix also comes with an (optional) Visual Studio Code color theme called “Flixify Dark”.

Features

• Semantic Syntax Highlighting

  • Code highlighting for *.flix files. This work best with the official vscode theme.

• Diagnostics

  • Compiler error messages.

• Auto-complete

  • Auto-complete as you type.
  • Auto-completion is context aware.
  • Type-directed completion of program holes.

• Snippets

  • Auto-complete common code constructs.

• Inlay Hints

  • Shows inline type information.

• Type and Effect Hovers

  • Hover over any expression to see its type and effect.
  • Hover over any local variable or formal parameter to see its type.
  • Hover over any function to see its type signature and documentation.

• Jump to Definition

  • Jump to the definition of any function.
  • Jump to the definition of any local variable or formal parameter.
  • Jump to the definition of any enum case.

• Find References

  • Find all references to a function.
  • Find all references to a local variable or formal parameter.
  • Find all references to an enum case.
  • Find all implementations of a trait.

• Symbols

  • List all document symbols.
  • List all workspace symbols.

• Rename

  • Rename local variables or formal parameters.
  • Rename functions.

• Code Lenses

  • Run main from within the editor.
  • Run tests from within the editor.

• Highlight

  • Highlights semantically related symbols.

• Semantic Tokens

  • Additional code highlighting hints provided by the compiler.

Known Limitations

• There is a known issue with PowerShell and using file names that contain special characters. We recommend that Flix source files are given only ASCII names.

• The extension assumes that you are working in “Workspace Mode”, i.e. you must have a folder open which contains your Flix source code.

• Upon startup, the Flix compiler has to load the entire Flix standard library into its caches which takes a few seconds.

Test Framework

Flix comes with a built-in test framework. A test is a Flix function marked with the @Test annotation. A test function must take no arguments and return Unit.

The Assert module provides assertion functions for testing. Here are the most commonly used:

The assertEq and assertNeq functions require a labelled argument expected / unexpected.

Here is an example:

use Assert.{assertEq, assertTrue, assertFalse, assertOk, assertErr}

def add(x: Int32, y: Int32): Int32 = x + y

def isEven(x: Int32): Bool = Int32.modulo(x, 2) == 0

def safeDivide(x: Int32, y: Int32): Result[String, Int32] =
    if (y == 0) Err("Division by zero") else Ok(x / y)

@Test
def testAdd01(): Unit \ Assert =
    assertEq(expected = 5, add(2, 3))

@Test
def testIsEven01(): Unit \ Assert =
    assertTrue(isEven(4))

@Test
def testIsEven02(): Unit \ Assert =
    assertFalse(isEven(3))

@Test
def testSafeDivide01(): Unit \ Assert =
    assertOk(safeDivide(10, 2))

@Test
def testSafeDivide02(): Unit \ Assert =
    assertErr(safeDivide(10, 0))

Running the tests (e.g. with flix test) yields:

Running 5 tests...

   PASS  testAdd01 1,4ms
   PASS  testIsEven01 312,5us
   PASS  testIsEven02 229,8us
   PASS  testSafeDivide01 366,0us
   PASS  testSafeDivide02 299,7us

Passed: 5, Failed: 0. Skipped: 0. Elapsed: 3,8ms.

Assertions with Custom Messages

Most assertions have WithMsg variants for custom error messages.

use Assert.{assertEqWithMsg, assertTrueWithMsg, assertFalseWithMsg}

@Test
def testAdd01(): Unit \ Assert =
    assertEqWithMsg(expected = 5, add(2, 3), "addition should work")

@Test
def testIsEven01(): Unit \ Assert =
    assertTrueWithMsg(isEven(4), "4 should be even")

@Test
def testIsEven02(): Unit \ Assert =
    assertFalseWithMsg(isEven(3), "3 should be odd")

@Test Function Signatures

A function marked with @Test must have one of the following signatures:

@Test
def test01(): Unit = ...
def test02(): Unit \ Assert = ...
def test03(): Unit \ Assert + IO = ...

In addition, a @Test function may use any algebraic effect for which there is a @DefaultHandler.

Build and Package Management

Flix comes with a build system and package manager. The build system makes it simple to compile a Flix program to a collection of Java classes and to build a fat JAR. The package manager makes it possible to create Flix packages, publish them on GitHub, and depend on them via a manifest file. The package manager also makes it possible to depend on Java JAR-artifacts published on Maven.

The Flix build system supports the following commands:

• init: creates a new Flix project in the current directory.
• check: checks the current project for compiler errors.
• build: builds the current project (i.e. emits Java bytecode).
• build-jar: builds a jar-file from the current project.
• build-fatjar: builds a jar-file with all dependencies bundled.
• build-pkg: builds a fpkg-file from the current project.
• run: runs main in current project.
• test: runs all tests in the current project.

All commands can be executed from the command line, from the REPL, and from VSCode.

All commands, except build-pkg work without a manifest file. To build, package, and publish a Flix project, a flix.toml manifest is required. The init command will create an empty skeleton flix.toml manifest, if not already present.

Project Structure

Flix scans for source files in the paths *.flix, src/**/*.flix,, and test/**/*.flix.

Flix scans for Flix packages and JARs in the paths lib/**/*.fpkg and lib/**/*.jar.

Build Management

We now discuss the build commands. Each command can be executed from the command line, from the REPL, and from VSCode.

Creating a New Project

We can create a new project, inside a directory, with the init command.

This will create the default Flix project structure:

.
├── flix.toml
├── LICENSE.md
├── README.md
├── src
│   └── Main.flix
└── test
    └── TestMain.flix

2 directories, 6 files

The most relevant files are flix.toml, src/Main.flix and test/TestMain.flix.

The flix.toml manifest file is discussed in the next section.

Tip: The init command is safe to use; it will only create files that do not already exist.

Checking a Project

We can check a project for compiler errors with the check command. During development, the check command is preferable to the build command because it skips code generation (and hence is significantly faster).

Building a Project

We can compile a project with the build command. Running the build command will compile the entire project and emit bytecode, i.e. compiled Java classes, to the build directory.

Flix has no clean command. Deleting the build directory serves the same purpose.

Building a JAR-file

We can compile a project to a JAR-file with the build-jar command. The build-jar command emits a artifact/project.jar file. If there is main function, we can run it:

$ java -jar artifact/project.jar

The JAR-file contains all class files from the build directory. The built JAR may depend on external JARs, if the project, or one of its dependencies, depends on JAR-files.

Note: build-jar automatically invokes the build command.

Building a fat JAR-file (bundling all dependencies)

We can compile a project to a single standalone fat JAR-file with the build-fatjar command. The build-fatjar command emits a artifact/project.jar file where all dependencies — both Flix and Maven — are bundled into one single JAR-file.

The JAR-file contains all class files from the build directory together with all class files extract from all Maven dependencies found in the lib directory.

Note: build-fatjar automatically invokes the build command.

Building a Flix Project

We can bundle a project into a Flix package file (fpkg) with the build-pkg command. Running the build-pkg command emits a artifact/project.fpkg file.

A Flix package file (fpkg) is essentially zip-file of the project source code. A Flix package, together with its flix.toml manifest, can be published on GitHub.

Running a Project

We do not have to build a JAR-file to run a project, we can simply use the run command which will compile and run the main entry point.

Testing a Project

We can use the test command to run all test cases in a project. Flix will collect all functions marked with @Test, execute them, and print a summary of the results:

Running 1 tests...

   PASS  test01 1,1ms

Passed: 1, Failed: 0. Skipped: 0. Elapsed: 3,9ms.

Package Management

Every non-trivial Flix project should have a flix.toml manifest. The manifest contains information about the project and its dependencies.

A minimal manifest is of the form:

[package]
name        = "hello-library"
description = "A simple library"
version     = "0.1.0"
flix        = "0.35.0"
license     = "Apache-2.0"
authors     = ["John Doe <john@example.com>"]

Note: The flix field is not yet used, but it will be used in the future.

Adding Flix Dependencies

We can add dependencies on other Flix packages to the manifest:

[dependencies]
"github:flix/museum"              = "1.4.0"
"github:magnus-madsen/helloworld" = "1.3.0"

Note: Flix requires version numbers to follow SemVer.

Adding Maven Dependencies

We can also add dependencies on Maven packages to the manifest:

[mvn-dependencies]
"org.junit.jupiter:junit-jupiter-api" = "5.9.2"

Understanding Dependency Resolution

Flix dependency resolution works as follows:

1. Flix reads flix.toml and computes the transitive set of Flix package dependencies.
2. Flix downloads all of these Flix packages.
3. Flix inspects each package for its Maven dependencies and downloads these.

We illustrate with an example. Assume we have a Flix package with:

[dependencies]
"github:flix/museum"              = "1.4.0"

Running Flix produces:

Found `flix.toml'. Checking dependencies...
Resolving Flix dependencies...
  Downloading `flix/museum.toml` (v1.4.0)... OK.
  Downloading `flix/museum-entrance.toml` (v1.2.0)... OK.
  Downloading `flix/museum-giftshop.toml` (v1.1.0)... OK.
  Downloading `flix/museum-restaurant.toml` (v1.1.0)... OK.
  Downloading `flix/museum-clerk.toml` (v1.1.0)... OK.
  Cached `flix/museum-clerk.toml` (v1.1.0).
Downloading Flix dependencies...
  Downloading `flix/museum.fpkg` (v1.4.0)... OK.
  Downloading `flix/museum-entrance.fpkg` (v1.2.0)... OK.
  Downloading `flix/museum-giftshop.fpkg` (v1.1.0)... OK.
  Downloading `flix/museum-restaurant.fpkg` (v1.1.0)... OK.
  Downloading `flix/museum-clerk.fpkg` (v1.1.0)... OK.
  Cached `flix/museum-clerk.fpkg` (v1.1.0).
Resolving Maven dependencies...
  Adding `org.apache.commons:commons-lang3' (3.12.0).
  Running Maven dependency resolver.
Dependency resolution completed.

This happens because flix/museum has the following dependency tree:

• flix/museum depends on:
  • flix/museum-entrance which depends on:
    • flix/museum-clerk
  • flix/museum-giftshop which depends on:
    • flix/museum-clerk
  • flix/museum-restaurant which depends on
    • org.apache.commons:commons-lang3

Security

To reduce the risk of supply-chain attacks, every dependency has a security context — even if you don’t set one explicitly. Security contexts control which language features a dependency may use. Broader security contexts enable more features but also increase the risk of supply-chain attacks.

The security contexts are defined as follows:

You can set the security context of each dependency in the manifest like so:

[dependencies]
"github:flix/museum"              = { version = "1.4.0", security = "plain" }
"github:magnus-madsen/helloworld" = { version = "1.3.0", security = "unrestricted" }

Security contexts are transitive: a dependency’s security context also applies to its transitive dependencies, unless a dependency explicitly declares a lesser security context. If multiple dependencies require the same library, the library inherits the most restrictive security context requested.

The recommended approach is to not specify a security context, thus defaulting to plain. It provides the best balance between flexibility and safety. You should avoid unrestricted when possible, as it permits (transitive) dependencies to do anything. Even building or compiling code that includes unrestricted dependencies can by itself expose you to a supply-chain attack.

If you are the author of a Flix library that requires effects, the best practice is to introduce your own custom effects instead of using the IO effect directly, and to split the library into two packages:

This approach provides several benefits:

• Most functionality remains in the trusted plain security context.
• Unsafe code is isolated in webserver-lib-handlers for easier review.
• Users can implement their own handlers if they don’t trust the provided ones.

Publishing a Package on GitHub

Flix packages are published on GitHub.

Automatically Publishing a Package

Flix can automatically package and publish artifacts on GitHub by following these steps:

1. Check that you have a flix.toml manifest (if not create one with init).
2. Check that the version field in flix.toml is correct.
3. Check that the repository field in flix.toml is correct. (e.g. repository = "github:user/repo")
4. Check that you have a GitHub token which has read and write access to Contents for the relevant repository.
   • If not go to GitHub and navigate to Settings > Developer settings > Personal access tokens and create a new token.
5. Run check and test to ensure that everything looks alright.
6. Run release --github-token <TOKEN>. You should see:

Found `flix.toml'. Checking dependencies...
Resolving Flix dependencies...
Downloading Flix dependencies...
Resolving Maven dependencies...
  Running Maven dependency resolver.
Downloading external jar dependencies...
Dependency resolution completed.
Release github:user/repo v1.2.3? [y/N]: y
Building project...
Publishing new release...

 Successfully released v1.2.3
 https://github.com/user/repo/releases/tag/v1.2.3

Tip: See the Museum Project for an example of a package that has been published on GitHub.

Tip: Flix will read the GitHub token from the environment variable GITHUB_TOKEN, if available.

Tip: Flix will also read the GitHub token from the file .GITHUB_TOKEN, if available.

Note: You cannot publish artifacts for empty GitHub repositories.

Warning: Be sure to keep your token safe!

Manually Publishing a Package

A package can also be manually published by following these steps:

1. Check that you have a flix.toml manifest (if not create one with init).
2. Check that the version field in flix.toml is correct.
3. Run check and test to ensure that everything looks correct.
4. Run build-pkg. Check that the artifact directory is populated.
5. Go to the repository on GitHub:
   1. Click “Releases”.
   2. Click “Draft new release”.
   3. Enter a tag of the form v1.2.3 (i.e. use SemVer).
   4. Upload the package.fpkg and flix.toml from the artifact directory.

Warning: You must upload both the package file (foo.fpkg) and the manifest file (flix.toml).

Finding Outdated Packages

We can use the outdated command to check if any Flix packages have updates available.

For example, if we have the following dependency in flix.toml:

[dependencies]
"github:flix/museum"            = "1.0.0"
"github:flix/museum-giftshop"   = "1.0.0"

then we can run outdated command which will produce:

Found `flix.toml`. Checking dependencies...
Resolving Flix dependencies...
  Cached `flix/museum.toml` (v1.0.0).
  Cached `flix/museum-giftshop.toml` (v1.0.0).  
  Cached `flix/museum-entrance.toml` (v1.0.0).  
  Cached `flix/museum-giftshop.toml` (v1.0.0).  
  Cached `flix/museum-restaurant.toml` (v1.0.0).
  Cached `flix/museum-clerk.toml` (v1.0.0).     
  Cached `flix/museum-clerk.toml` (v1.0.0).
Downloading Flix dependencies...
  Cached `flix/museum.fpkg` (v1.0.0).
  Cached `flix/museum-giftshop.fpkg` (v1.0.0).
  Cached `flix/museum-entrance.fpkg` (v1.0.0).
  Cached `flix/museum-giftshop.fpkg` (v1.0.0).
  Cached `flix/museum-restaurant.fpkg` (v1.0.0).
  Cached `flix/museum-clerk.fpkg` (v1.0.0).
  Cached `flix/museum-clerk.fpkg` (v1.0.0).
Resolving Maven dependencies...
  Running Maven dependency resolver.
Downloading external jar dependencies...
Dependency resolution completed.

package                 current    major    minor    patch
flix/museum             1.0.0               1.4.0         
flix/museum-giftshop    1.0.0               1.1.0         

The outdated command tells us that we are using two packages which have updates available:

• flix/museum can be upgraded from 1.0.0 to 1.4.0.
• flix/museum-giftshop can be upgraded from 1.0.0 to 1.1.0.

If we want to upgrade a package, we must manually modify flix.toml.

Advanced Features

In this chapter, we discuss some advanced features of Flix, including:

• Checked Casts and Unchecked Casts
• The bug! and unreachable! functions
• Purity Reflection
• Termination Checking

Checked Type and Effect Casts

The Flix type and effect system – by design – does not support sub-typing nor sub-effecting. To work around these limitations, which are rare in practice, Flix has two safe upcast constructs:

• A checked type cast: checked_cast(exp), and
• A checked effect cast checked_ecast(exp).

Note: The checked_cast and checked_ecast expressions are guaranteed to be safe. The Flix compiler will check at compile-time that every checked cast cannot go wrong.

Checked Type Casts

The following program:

import java.lang.Object

def main(): Unit =
    let s = "Hello World";
    let _: Object = s;
    ()

does not compile:

❌ -- Type Error --------------------------------------------------

>> Unexpected type: expected 'java.lang.Object', found 'String'.

5 |     let _: Object = s;
                        ^
                        expression has unexpected type.

because in Flix the String type is not a subtype of Object.

We can use a checked type cast to safely upcast from String to Object:

import java.lang.Object;

def main(): Unit =
    let s = "Hello World";
    let _: Object = checked_cast(s);
    ()

We can use the checked_cast construct to safely upcast any Java type to one of its super-types:

let _: Object       = checked_cast("Hello World");
let _: CharSequence = checked_cast("Hello World");
let _: Serializable = checked_cast("Hello World");
let _: Object       = checked_cast(null);
let _: String       = checked_cast(null);

Checked Effect Casts

The following program:

def hof(f: Int32 -> Int32 \ IO): Int32 \ IO = f(42)

def main(): Int32 \ IO =
    hof(x -> x + 1)

does not compile:

❌ -- Type Error --------------------------------------------------

>> Expected argument of type 'Int32 -> Int32 \ IO', but got 'Int32 -> Int32'.

4 |     hof(x -> x + 1)
            ^^^^^^^^^^
            expected: 'Int32 -> Int32 & Impure \ IO'

The function 'hof' expects its 1st argument to be of type 'Int32 -> Int32 \ IO'.

Expected: Int32 -> Int32 & Impure \ IO
  Actual: Int32 -> Int32

because in Flix a pure function is not a subtype of an impure function. Specifically, the hof requires a function with the IO effect, but we are passing in a pure function.

We can use a checked effect cast to safely upcast a pure expression to an impure expression:

def main(): Int32 \ IO =
    hof(x -> checked_ecast(x + 1))

The checked_ecast construct allows us to pretend that x + 1 has the IO effect.

Note: In Flix – as a general rule – higher-order functions should not require their function arguments to have a specific effect. Instead they should be effect polymorphic.

Function Types

Neither the checked_cast nor the checked_ecast constructs work on function types.

For example, the following does not work:

let f: Unit -> ##java.lang.Object = checked_cast(() -> "Hello World")

because it tries to cast the function type Unit -> String to Unit -> Object.

Instead, we should write:

let f: Unit -> ##java.lang.Object = (() -> checked_cast("Hello World"))

because it directly casts String to Object.

Unchecked Type and Effect Casts

Flix also supports unchecked type and effect casts.

Unchecked Type Casts

An unchecked type cast instructs the compiler that an expression has a specific type.

Warning: Type casts are very dangerous and should be used with utmost caution!

Flix programmers should normally never need to use an unchecked type cast.

Example: Safe Cast to a Super-Type

The expression below casts a String to an Object:

unchecked_cast("Hello World" as Object)

Note: It is safer to use the checked_cast expression.

Example: Safe Cast from Null to an Object-Type

The expression below casts the null value (of type Null) to String:

unchecked_cast(null as String)

Note: It is safer to use the checked_cast expression.

Example: Unsafe Type Cast

The expression below contains an illegal cast and triggers a ClassCastException at runtime:

unchecked_cast((123, 456) as Integer)

Effect Casts

An unchecked effect cast instructs the compiler that an expression has a specific effect.

Warning: Effect casts are extremely dangerous and should be used with extreme caution!

Flix programmers should normally never need to use an unchecked effect cast.

Example: Unsafe Effect Cast

We can pretend an impure expression is pure:

def main(): Unit =
    unchecked_cast(println("Hello World") as _ \ {})

Here we call println which has the IO effect and then we explicitly, and unsafely, cast away the effect, pretending that the expression is pure.

Warning: Never cast effectful expressions to pure. You have been warned.

bug! and unreachable!

Flix supports two special “functions”: bug! and unreachable! that can be used to indicate when an internal program invariant is broken and execute should abort. For example:

match o {
    case Some(x) => ...
    case None    => bug!("The value of `o` cannot be empty.")
}

As another example:

match k {
    case n if n == 0 => ...
    case n if n >= 0 => ...
    case n if n <= 0 => ...
    case n           =>  unreachable!()
}

Use of bug! and unreachable! should be avoided whenever possible.

Laziness

Flix uses eager evaluation in most circumstances, but allows the programmer to opt-in to lazy evaluation when appropriate with the lazy keyword:

let x: Lazy[Int32] = lazy (1 + 2);

The expression won’t be evaluated until it’s forced:

let y: Int32 = force x;

Note: The lazy construct requires the expression it’s given to be pure.

Note: Forcing a lazy value that’s already been evaluated won’t evaluate it for a second time.

Lazy data structures

Laziness can be used to create lazy data structures which are evaluated as they’re used. This even allows us to create infinite data structures.

Here for example, is a data structure which implements an infinitely long stream of integers which increase by one each time:

mod IntStream {

    enum IntStream { case SCons(Int32, Lazy[IntStream]) }

    pub def from(x: Int32): IntStream =
        IntStream.SCons(x, lazy from(x + 1))
}

Given this, we can implement functions such as map and take:

    pub def take(n: Int32, s: IntStream): List[Int32] =
        match n {
            case 0 => Nil
            case _ => match s {
                case SCons(h, t) => h :: take(n - 1, force t)
            }
        }

    pub def map(f: Int32 -> Int32, s: IntStream): IntStream =
        match s {
            case SCons(h, t) => IntStream.SCons(f(h), lazy map(f, force t))
        }

So, for example:

IntStream.from(42) |> IntStream.map(x -> x + 10) |> IntStream.take(10)

Will return:

52 :: 53 :: 54 :: 55 :: 56 :: 57 :: 58 :: 59 :: 60 :: 61 :: Nil

Flix provides DelayList and DelayMap data structures which already implement this functionality and more:

DelayList.from(42) |> DelayList.map(x -> x + 10) |> DelayList.take(10)

Purity Reflection

Note: This is an advanced feature and should only be used by experts.

Purity reflection enables higher-order functions to inspect the purity of their function arguments.

This allows us to write functions that use selective lazy and/or parallel evaluation.

For example, here is the implementation of Set.count:

@ParallelWhenPure
pub def count(f: a -> Bool \ ef, s: Set[a]): Int32 \ ef =
    match purityOf(f) {
        case Purity.Pure(g) =>
            if (useParallelEvaluation(s))
                let h = (k, _) -> g(k);
                let Set(t) = s;
                RedBlackTree.parCount(h, t)
            else
                foldLeft((b, k) -> if (f(k)) b + 1 else b, 0, s)
        case Purity.Impure(g) => foldLeft((b, k) -> if (g(k)) b + 1 else b, 0, s)
    }

Here the purityOf function is used to reflect on the purity of f:

• If f is pure then we evaluate Set.count in parallel over the elements of the set (if the set is big enough to warrant it).
• If f is effectful then we use an ordinary (single-threaded) fold.

The advantage is that we get parallelism for free – if f is pure.

Type-Level Programming

Note: This feature is experimental. Do not use in production.

This section assumes prior familiarity with type-level programming and phantom types.

Type-Level Booleans

A unique Flix feature is its support for type-level Boolean formulas. This means true and false are types, but also that formulas such as x and (not y) are types. A type-level Boolean formula has kind Bool. Two type-level Boolean formulas are equal if the formulas are equivalent (i.e. have the same truth tables). For example, the two types true and x or not x are the same type.

While type-level Boolean formulas are not as expressive as general refinement types or dependent types they support complete type inference and parametric polymorphism. This means that they are very ergonomic to work with.

We can use type-level Boolean formulas to statically enforce program invariants.

We illustrate with a few examples:

Humans and Vampires

///
/// We can use a phantom type-level Boolean to model whether a person is alive
/// or is undead (i.e. a vampire).
///
enum Person[_isAlive: Bool] {
    /// A person has a name, an age, and is modelled as a record.
    case P({name = String, age = Int32})
}

///
/// We interpret the Boolean `true` is alive and the Boolean `false` as undead
/// (i.e. a vampire).
///
type alias Alive  = true
type alias Undead = false

///
/// A person who is born is alive.
///
def born(name: String): Person[Alive] =
    Person.P({name = name, age = 0})

///
/// A person who is alive and is bitten becomes a vampire.
///
/// Note that the type system enforces that an already undead (i.e. a vampire)
/// cannot be bitten again.
///
def bite(p: Person[Alive]): Person[Undead] = match p {
    /// The implementation is not important; it simply restructs the person.
    case Person.P(r) => Person.P(r)
}

///
/// Two persons can be married, but only if they are both alive or both undead.
///
/// (The church does not yet recognize human-vampire marriages.)
///
/// Note that the type system enforces that both arguments have the same type.
///
def marry(_p1: Person[isAlive], _p2: Person[isAlive]): Unit = ()

///
/// We can implement a more sophisticated version of born.
///
/// If two persons have a child then that child is a vampire if one of them is.
///
/// Note that here we use the type-level computation `isAlive1 and isAlive2`
/// to compute whether the result is alive or undead.
///
def offspring(p1: Person[isAlive1], p2: Person[isAlive2]): Person[isAlive1 and isAlive2] =
    match (p1, p2) {
        case (Person.P(r1), Person.P(r2)) =>
            Person.P({name = "Spawn of ${r1#name} and ${r2#name}", age = 0})
}

///
/// A person can age-- no matter if they are alive or undead.
///
/// Note that this function preserves the `isAlive` parameter. That is, if a
/// person is alive they stay alive.
///
def birthday(p: Person[isAlive]): Person[isAlive] = match p {
    case Person.P(r) => Person.P({name = r#name, age = r#age + 1})
}

We can now illustrate how the type system enforces certain invariants.

For example, the type system ensures that person cannot be bitten twice:

let p = birthday(bite(born("Dracula")));
bite(p);

If we compile this program then the Flix compiler emits a compiler error:

❌ -- Type Error --------------------------------------------------

>> Expected argument of type 'Person[true]', but got 'Person[false]'.

69 |     bite(p);
              ^
              expected: 'Person[true]'

The function 'bite' expects its 1st argument to be of type 'Person[true]'.

Here we have to recall that true means Alive and false means Undead.

Termination Checking

Flix supports the @Terminates annotation, which asks the compiler to verify that a function is structurally recursive — meaning it is guaranteed to terminate on all inputs. A function annotated with @Terminates must make recursive calls only on strict substructures of its formal parameters. The compiler checks this at compile time and reports an error if the function does not satisfy the structural recursion requirement.

Structural Recursion

The core idea behind @Terminates is structural recursion: every recursive call must pass an argument that was obtained by pattern matching on a formal parameter and extracting a component from inside a constructor. This component is strictly smaller than the original, so the recursion must eventually reach a base case.

For example, here is a structurally recursive length function on a custom list type:

enum MyList[a] {
    case Nil
    case Cons(a, MyList[a])
}

@Terminates
def length(l: MyList[Int32]): Int32 = match l {
    case MyList.Nil         => 0
    case MyList.Cons(_, xs) => 1 + length(xs)
}

The recursive call passes xs, which is bound inside the Cons constructor of l. Since xs is strictly smaller than l, the compiler accepts this function.

Tree Recursion

Structural recursion works on any algebraic data type, not just lists. A function may make multiple recursive calls in the same branch, as long as each call receives a strict substructure of a formal parameter.

For example, here is a size function on a binary tree:

enum MyTree[a] {
    case Leaf(a)
    case Node(MyTree[a], MyTree[a])
}

@Terminates
def size(t: MyTree[Int32]): Int32 = match t {
    case MyTree.Leaf(_)    => 1
    case MyTree.Node(l, r) => size(l) + size(r)
}

Both l and r are bound inside the Node constructor of t, so both recursive calls are valid.

Multiple Parameters

When a function has multiple parameters, only one parameter needs to decrease per recursive call. The other parameters may be passed unchanged.

For example, append recurses on l1 while passing l2 unchanged:

enum MyList[a] {
    case Nil
    case Cons(a, MyList[a])
}

@Terminates
def append(l1: MyList[Int32], l2: MyList[Int32]): MyList[Int32] = match l1 {
    case MyList.Nil         => l2
    case MyList.Cons(x, xs) => MyList.Cons(x, append(xs, l2))
}

The compiler sees that xs is a strict substructure of l1, which is sufficient. The fact that l2 does not decrease is fine.

Warning: @Terminates guarantees that a function terminates, but it does not guarantee that it is tail recursive. For example, the append function above is structurally recursive but not tail recursive — the recursive call is wrapped in MyList.Cons(x, ...). This means it can overflow the stack on very long lists. See the Tail Recursion section for how to write stack-safe recursive functions.

Local Definitions

Local definitions inside a @Terminates function are checked independently. A local function may recurse on its own parameters:

enum MyList[a] {
    case Nil
    case Cons(a, MyList[a])
}

@Terminates
def length(l: MyList[Int32]): Int32 =
    def loop(ll: MyList[Int32], acc: Int32): Int32 = match ll {
        case MyList.Nil         => acc
        case MyList.Cons(_, xs) => loop(xs, acc + 1)
    };
    loop(l, 0)

Here loop recurses on its own parameter ll, passing xs which is a strict substructure. The outer function length is non-recursive, so it is trivially terminating.

Higher-Order Functions

A @Terminates function may apply closures that come from its formal parameters. This allows higher-order patterns like map:

enum MyList[a] {
    case Nil
    case Cons(a, MyList[a])
}

@Terminates
def map(f: Int32 -> Int32, l: MyList[Int32]): MyList[Int32] = match l {
    case MyList.Nil         => MyList.Nil
    case MyList.Cons(x, xs) => MyList.Cons(f(x), map(f, xs))
}

The application f(x) is allowed because f is a formal parameter of map. The compiler tracks that f originates from a parameter and permits the call.

However, applying a locally-constructed closure is forbidden:

@Terminates
def bad(x: Int32): Int32 =
    let c = y -> y + 1;
    c(x)

This is rejected because c is not a formal parameter — it is a locally defined closure that could, in general, hide arbitrary computation.

Warning: @Terminates guarantees that map terminates assuming its function argument f also terminates. If f is a non-terminating function, then map may not terminate either. The annotation only verifies the structural recursion of map itself — it does not check the behavior of f.

Calling Other Functions

A @Terminates function may only call other functions that are also annotated with @Terminates. Calling a function without the annotation is an error.

For example, the following is rejected:

def g(x: Int32): Int32 = x * 2

@Terminates
def f(x: Int32): Int32 = g(x)

The compiler reports:

>> Call to non-@Terminates function 'g' in @Terminates function 'f'.

   ... g(x)
       ^^^^^^^^^
       non-terminating call

The fix is to annotate the callee:

@Terminates
def g(x: Int32): Int32 = x * 2

@Terminates
def f(x: Int32): Int32 = g(x)

Strict Positivity

Enum types used for structural recursion must be strictly positive. A type is strictly positive if it does not contain a recursive occurrence to the left of an arrow in any constructor.

For example, the following enum is not strictly positive because Bad appears to the left of -> in the argument to MkBad:

enum Bad {
    case MkBad(Bad -> Int32)
}

@Terminates
def f(x: Bad): Int32 = match x {
    case Bad.MkBad(_) => 0
}

The compiler rejects this with:

>> Non-strictly positive type in 'f'.

   ... case MkBad(Bad -> Int32)
                  ^^^^^^^^^^^^
                  negative occurrence

Common Errors

The most common mistake is passing the original parameter instead of a substructure obtained from pattern matching:

enum MyList[a] {
    case Nil
    case Cons(a, MyList[a])
}

@Terminates
def f(x: MyList[Int32]): Int32 = match x {
    case MyList.Nil         => 0
    case MyList.Cons(_, xs) => f(x)
}

Notice that the recursive call passes x (the original parameter) instead of xs (the tail extracted from the pattern). The compiler reports:

>> Non-structural recursion in 'f'.

   ... f(x)
       ^^^^
       non-structural recursive call

   Parameter   Argument   Status
   x           x          alias of 'x' (not destructured)

The diagnostic table shows which arguments are problematic. The fix is to pass xs instead of x:

case MyList.Cons(_, xs) => f(xs)

Common Problems

• ToString is not defined on ‘a’
• Records and Complex Instances
• Expected kind ‘Bool or Effect’ here, but kind ‘Type’ is used

ToString is not defined on ‘a’

Given the program:

def main(): Unit \ IO =
    let l = Nil;
    println(l)

The Flix compiler reports:

❌ -- Type Error ---------------------

>> ToString is not defined on a. [...]

3 |     println(l)
        ^^^^^^^^^^
        missing ToString instance

The issue is that the empty list has the polymorphic type: List[a] for any a. This means that Flix cannot select the appropriate ToString trait instance.

The solution is to specify the type of the empty list. For example, we can write:

def main(): Unit \ IO =
    let l: List[Int32] = Nil;
    println(l)

which solves the problem because Flix can find an instance of ToString trait for the concrete type List[Int32].

Records and Complex Instances

Given the program:

instance Eq[{fstName = String, lstName = String}]

The Flix compiler reports:

❌ -- Instance Error --------------------------------------------------

>> Complex instance type '{ fstName = String, lstName = String }' in 'Eq'.

1 | instance Eq[{fstName = String, lstName = String}]
             ^^
             complex instance type

This is because, at least for the moment, it is not possible to define trait instances on records (or Datalog schema rows). This may change in the future. Until then, it is necessary to wrap the record in an algebraic data type. For example:

enum Person({fstName = String, lstName = String})

and then we can implement Eq for the Person type:

instance Eq[Person] {
    pub def eq(x: Person, y: Person): Bool =
        let Person(r1) = x;
        let Person(r2) = y;
        r1#fstName == r2#fstName and r1#lstName == r2#lstName
}

Expected kind ‘Bool or Effect’ here, but kind ‘Type’ is used

Given the program:

enum A[a, b, ef] {
    case A(a -> b \ ef)
}

The Flix compiler reports:

❌ -- Kind Error -----------------------------------------------

>> Expected kind 'Bool or Effect' here, but kind 'Type' is used.

2 |     case A(a -> b \ ef)
                        ^^
                        unexpected kind.

Expected kind: Bool or Effect
Actual kind:   Type

This is because Flix assumes every un-annotated type variable to have kind Type. However, in the above case a and b should have kind Type, but ef should have kind Bool. We can make this explicit like so:

enum A[a: Type, b: Type, ef: Bool] {
    case A(a -> b \ ef)
}

Frequently Asked Questions

Does Flix supports constants?

Yes and no. Flix does not support top-level constants. You can, however, declare a pure function which takes zero arguments:

def pi(): Float64 = 3.14f64

The Flix compiler will inline such constants.

If you have an expensive computation that you want to perform once, you should compute it where needed and explicitly pass it around. Flix does not support top-level constants because they violate the principle that no code should be executed before main.

Glossary

Algebraic Data Type. A data type defined using sum and product types, i.e. using enumerated types and tuple types.

Algebraic Effect. A user-defined effect which can be handled. The handler is supplied with the (delimited) continuation of the effect. The continuation can be dropped, resume once, or resumed multiple-times.

Associated Type. A type that belongs to a trait. Each trait instance specifies the specific associated type for that instance. Hence different trait instances can have different associated types.

Associated Effect. An effect that belongs to a trait. Each trait instance specifies the specific associated effect for that instance. Hence different trait instances can have different associated effects.

Checked Cast. A safe cast that the compiler ensures is correct. Cannot fail at runtime.

Effect. Flix supports three types of effects: built-in effects (e.g. IO and NonDet), region-based effects, and user-defined effects.

Effect Cast. A cast that changes the effect of an expression.

Effect Member. See associated effect.

Effect Polymorphic. A function whose effect(s) depend on the effect(s) of its function argument. See also higher-order function.

Effect Handler. An expression which handles a user-defined effect.

Higher-Order Function. A function that takes a function argument or returns a function.

IO Effect. A built-in generic effect which represents any interaction with the outside world.

Pure. A function (or expression) which has no effects.

String Interpolation. A language feature that allows a string to contain expressions.

Tail Call. A function call in tail-position and hence does not require additional stack space.

Trait. An interface that specifies a collection of function signatures and default functions. A trait can be implemented by several data types. Traits in Flix are type classes.

Type Class. See Trait.

Type Cast. A cast that changes the type of an expression.

Type Inference. A language feature that allows the compiler to infer the type of an expression without requiring annotations from the programmer.

Type Member. See associated type.

Unchecked Cast. An unsafe cast which is not verified by the compiler. Can fail at runtime.

Uninterpretable Effect. An effect that cannot (or should not) be handled, e.g. IO.

Additional Information

More information about the Flix programming language can be found in:

• The research literature written by programming language researchers.
• A series of blog posts written by the community.
• A page for LLMs describing changes to Flix since older research papers, talks, and blog posts.

Getting Help

If you have a question or comment we are happy to help you out on our Gitter channel:

https://gitter.im/flix/Lobby

Reporting a Bug

If you encounter a bug, you can report it here:

https://github.com/flix/flix/issues

but first you may wish to talk to us on Gitter.

Research Literature

The following research papers cover specific aspects of Flix:

• The Principles of the Flix Programming Language
• Flix: A Meta Programming Language for Datalog
• Relational Nullable Types with Boolean Unification
• Fixpoints for the Masses: Programming with First-Class Datalog Constraints
• Polymorphic Types and Effects with Boolean Unification
• Implicit Parameters for Logic Programming
• Safe and Sound Program Analysis with Flix
• Tail Call Elimination and Data Representation for Functional Languages on the Java Virtual Machine
• From Datalog to Flix: A Declarative Language for Fixed Points on Lattices
• Programming a Dataflow Analysis in Flix

Blog Posts

A few people are writing about various aspects of Flix on their blogs:

Valentin Erokhin is writing blog posts on effect handlers and Flix:

• Algebraic Effects in Practice with Flix

Paul Butcher is writing a blog post series on Flix:

• An introduction to Datalog in Flix: Part 1
• An introduction to Datalog in Flix: Part 2
• An introduction to Datalog in Flix: Part 3
• An introduction to Datalog in Flix: Part 4

Susan Potter is writing a blog post series on Flix:

• Getting Started with Flix, Part 0
• Higher-order functions & infix combinators, Part 1

Jesse Claven wrote a blog post on logic programming in Flix:

• Programming: Imperative to Functional to Logic

Magnus Madsen wrote a few blog posts on Flix during COVID:

• Effect Systems vs Print Debugging: A Pragmatic Solution
• In Defense of Programming Languages
• Taming Impurity with Polymorphic Effects
• Naming Functional and Destructive Operations
• Redundancies as Compile-Time Errors
• Design Flaws in Flix

Lutz Hühnken wrote a blog post on Flix for Java progammers:

• Flix For Java Programmers

Varun Gandhi wrote a critical blog post about the value of effects, using Flix as an example:

• On the purported benefits of effect systems

Magnus Madsen did an interview about Flix on the Happy Path Programming podcast:

• Episode 54 Flix: Designing a principled programming language with Magnus Madsen

Videos

A collection of videos about Flix.

Industry Talks

• Magnus Madsen @ LambdaDays 2025: An Introduction to Effectful Programming in Flix (slides)
• Magnus Madsen @ Devoxx Greece 2025: Effectful Programming in the Flix Programming Language (slides)
• Magnus Madsen @ Goto 2023: An Introduction to Functional Imperative Programming in Flix

Research Talks

• Matthew Lutze @ PLDI 2024: Associated Effects: Flexible Abstractions for Effectful Programming
• Matthew Lutze @ ICFP 2023:With or Without You: Programming with Effect Exclusion
• Magnus Madsen @ Onward 2022: The Principles of the Flix Programming Language

For LLMs

Beep boop! This page is just for you, dear LLM. But if a human has stumbled in here — hello! Make yourself at home. We won’t tell anyone.

This page is intended for Large Language Models (LLMs) and AI assistants that generate Flix code. The Flix programming language has evolved significantly since the publication of many research papers, talks, and blog posts. If you are an LLM, you may have been trained on outdated Flix code. This section describes the most important changes.

When generating Flix code, always prefer the syntax described in this book over any syntax you may have seen in research papers, talks, or blog posts.

The Signature of main

The main function must take zero arguments and return Unit. It must be effectful.

❌ Old (no longer valid):

def main(args: Array[String]): Int32 & IO = ... // Wrong -- Outdated

✅ Current (correct, as of Flix 0.68.0):

def main(): Unit \ IO =
    println("Hello World!")

The main function can use IO, NonDet, or any effect with a default handler (e.g. Env, Exit, Clock). Command line arguments are accessed via Env.getArgs(), not via a parameter. See The Main Function for details.

Effect Syntax Uses \ Not &

Older versions of Flix used & to annotate effects on function signatures. The current syntax uses \ (backslash).

❌ Old (no longer valid):

def divide(x: Int32, y: Int32): Int32 & DivByZero = ... // Wrong -- Outdated
def main(): Unit & IO = ...                             // Wrong -- Outdated

✅ Current (correct, as of Flix 0.68.0):

def divide(x: Int32, y: Int32): Int32 \ DivByZero = ...
def main(): Unit \ IO = ...

Note: Always use \ (backslash) for effects, never &.

No do Keyword for Effect Operations

Older versions of Flix required the do keyword to call an effect operation. This is no longer the case. Effect operations are called like regular functions using the Effect.operation() syntax.

❌ Old (no longer valid):

eff DivByZero {
    def divByZero(): Void
}

def divide(x: Int32, y: Int32): Int32 \ DivByZero =
    if (y == 0) do DivByZero.divByZero() else x / y // Wrong -- Outdated

✅ Current (correct, as of Flix 0.68.0):

eff DivByZero {
    def divByZero(): Void
}

def divide(x: Int32, y: Int32): Int32 \ DivByZero =
    if (y == 0) DivByZero.divByZero() else x / y

Note: Simply call DivByZero.divByZero() without the do keyword.

Effect Handler Syntax: run/with handler

Older versions of Flix used run { ... } with Effect { ... } to handle effects. The current syntax requires the handler keyword: run { ... } with handler Effect { ... }.

❌ Old (no longer valid):

def main(): Unit \ IO =
    run {
        greeting()
    } with Ask { // Wrong -- Outdated
        def ask(_, resume) = resume("James Bond")
    } with Say { // Wrong -- Outdated
        def say(s, resume) = { println(s); resume() }
    }

✅ Current (correct, as of Flix 0.68.0):

def main(): Unit \ IO =
    run {
        greeting()
    } with handler Ask {
        def ask(_, k) = k("James Bond")
    } with handler Say {
        def say(s, k) = { println(s); k() }
    }

Note: Always write with handler EffectName, not just with EffectName. Multiple handlers are chained: with handler A { ... } with handler B { ... }.

Don’t Nest run Blocks

When handling multiple effects, use a single run block with chained with handler clauses. Do not nest run blocks inside each other.

❌ Incorrect:

use Math.Random
use Time.Duration.{seconds}
use Time.Sleep

def main(): Unit \ { Logger, Random, Sleep, IO } =
    run {
        run {
            println("Sleeping 3 times with ±20% jitter...");
            Sleep.sleep(seconds(1));
            Sleep.sleep(seconds(2));
            Sleep.sleep(seconds(3));
            println("Done!")
        } with Sleep.withJitter(0.2)
    } with Sleep.withLogging

✅ Correct:

use Math.Random
use Time.Duration.{seconds}
use Time.Sleep

def main(): Unit \ { Logger, Random, Sleep, IO } =
    run {
        println("Sleeping 3 times with ±20% jitter...");
        Sleep.sleep(seconds(1));
        Sleep.sleep(seconds(2));
        Sleep.sleep(seconds(3));
        println("Done!")
    } with Sleep.withJitter(0.2)
      with Sleep.withLogging

Note: A single run block can have multiple with handler clauses chained one after another. There is no need to nest run blocks.

Don’t Write CPS — Use Effects and Handlers

Do not simulate effects by writing continuation-passing style (CPS) code where handler functions take callbacks. Flix has a built-in effect system — use run/with handler blocks instead.

❌ Incorrect (manual CPS with nested callbacks):

def handleSleep(f: Unit -> a \ { Sleep, ef }): a \ ef + IO = ...

def withLogging(f: Unit -> a \ { Sleep, ef }): a \ ef + { Sleep, Logger } = ...

def withJitter(factor: Float64, f: Unit -> a \ { Sleep, ef }): a \ ef + { Sleep, Random } = ...

def main(): Unit \ { Logger, Random, Sleep, IO } =
    handleSleep(() ->
        withLogging(() ->
            withJitter(0.2, () ->
                println("Sleeping 3 times with ±20% jitter...");
                Sleep.sleep(seconds(1));
                Sleep.sleep(seconds(2));
                Sleep.sleep(seconds(3));
                println("Done!")
            )
        )
    )

✅ Correct (effects and handlers):

use Math.Random
use Time.Duration.{seconds}
use Time.Sleep

def main(): Unit \ { Logger, Random, Sleep, IO } =
    run {
        println("Sleeping 3 times with ±20% jitter...");
        Sleep.sleep(seconds(1));
        Sleep.sleep(seconds(2));
        Sleep.sleep(seconds(3));
        println("Done!")
    } with Sleep.withJitter(0.2)
      with Sleep.withLogging

Note: Effects and handlers let you write flat, sequential code. Use run { ... } with Handler.middleware to compose handlers — never pass callbacks to simulate what the effect system already provides.

Java Types Must Be Imported

In Flix, Java classes must always be imported before they can be used. You cannot use fully-qualified Java class names inline. Use import declarations at the top of your file or module.

❌ Old (no longer valid):

def main(): Unit \ IO =
    let f = new java.io.File("foo.txt"); // Wrong -- Outdated
    println(f.getName())

✅ Current (correct, as of Flix 0.68.0):

import java.io.File

def main(): Unit \ IO =
    let f = new File("foo.txt");
    println(f.getName())

Note: Always import the class first, then use its short name.

No Old-Style import for Java Methods

Older versions of Flix used a special import syntax inside function bodies to access Java constructors, methods, and static methods. This syntax no longer exists. Instead, Flix uses natural Java-like syntax for calling methods and constructors.

❌ Old (no longer valid):

def area(w: Int32, h: Int32): Int32 =
    import static java.lang.Math.abs(Int32): Int32 \ {}; // Wrong -- Outdated
    abs(w * h)

✅ Current (correct, as of Flix 0.68.0):

import java.lang.Math

def area(w: Int32, h: Int32): Int32 =
    unsafe Math.abs(w * h)

Similarly, object methods are called with regular dot syntax:

❌ Old (no longer valid):

def getLength(f: ##java.io.File): Int64 =        // Wrong -- Outdated
    import java.io.File.length(): Int64 \ {};     // Wrong -- Outdated
    length(f)

✅ Current (correct, as of Flix 0.68.0):

import java.io.File

def getLength(f: File): Int64 =
    unsafe f.length()

Note: Import the class at the top level and then call methods with standard dot syntax. Use unsafe blocks only when you know the Java method is pure. All Java interop has the IO effect by default. See Calling Methods for more details.

Annotations Are Uppercase

Flix annotations use uppercase names.

❌ Old (no longer valid):

@test                                    // Wrong -- Outdated
def testAdd01(): Bool = 1 + 2 == 3      // Wrong -- Outdated

✅ Current (correct, as of Flix 0.68.0):

@Test
def testAdd01(): Unit \ Assert =
    Assert.assertEq(expected = 3, 1 + 2)

Note: Use @Test, not @test. Other annotations are similarly uppercase, e.g. @Parallel, @Lazy, @MustUse.

Datalog inject Requires Arity

Older versions of Flix allowed inject without specifying the arity of the predicate. The current syntax requires the arity using the Predicate/N notation.

❌ Old (no longer valid):

let edges = inject s into Edge; // Wrong -- Outdated

✅ Current (correct, as of Flix 0.68.0):

let edges = inject s into Edge/2;

The general form is Predicate/Arity. When injecting multiple collections, each predicate requires its arity:

let p = inject names, jedis into Name/1, Jedi/1;

No rel or lat Declarations for Datalog

Older versions of Flix required explicit rel and lat declarations to introduce predicate symbols for Datalog constraints. This is no longer the case. Predicate symbols are inferred from use and do not need to be declared.

❌ Old (no longer valid):

rel Edge(x: Int32, y: Int32) // Wrong -- Outdated
rel Path(x: Int32, y: Int32) // Wrong -- Outdated

✅ Current (correct, as of Flix 0.68.0):

Predicate symbols like Edge and Path are simply used directly in Datalog rules and facts without any declaration:

def reachable(s: Set[(Int32, Int32)], src: Int32, dst: Int32): Bool =
    let rules = #{
        Path(x, y) :- Edge(x, y).
        Path(x, z) :- Path(x, y), Edge(y, z).
    };
    let edges = inject s into Edge/2;
    let paths = query edges, rules select true from Path(src, dst);
    not (paths |> Vector.isEmpty)

Note: The predicate symbols Edge and Path do not have to be explicitly introduced; they are simply used. Similarly, for lattice semantics, no lat declaration is needed.